Introdução

Este livro tem as resoluções das provas dos concursos do Colégio Militar de Curitiba para ingresso no 6º ano do Ensino Fundamental.

Cada capítulo é uma prova e cada subcapítulo uma questão. Manterei sempre as provas mais recentes primeiro. As resoluções ficam inicialmente ocultas, para que você possa imprimir o livro sem elas, e posteriormente conferir as respostas.

Provas e gabaritos disponíveis em https://www.concursosmilitares.com.br/provas-anteriores/exercito/colegio-militar/curitiba/

Elaborado com a ferramenta mdBook, que facilita a escrever e publicar este livro por partes e tem integração com o github.

2020/2021

Esta prova pode ser baixada em https://www.concursosmilitares.com.br/provas-anteriores/exercito/colegio-militar/curitiba/cmc-2020-2021-matematica-fundamental.pdf

O gabarito oficial pode ser baixado em https://www.concursosmilitares.com.br/provas-anteriores/exercito/colegio-militar/curitiba/cmc-2020-2021-gabarito-fundamental.pdf

Porém estou disponibilizando a prova aqui caso tenha algum problema de acesso no link original e o gabarito aqui

Questão 1

A professora Ana possui apenas 10 (dez) alunos em sua classe. Com o início da pandemia, as aulas passaram a ocorrer de forma remota, por meio de vídeos, lives¹ e chats². Em uma avaliação, apenas um dos alunos dessa classe obteve nota 10,0 (dez) e os demais obtiveram nota 9,0 (nove).

Qual foi a média aritmética das notas desses 10 (dez) alunos?

(A) 9,0

(B) 9,5

(D) 9,1

(E) 9,9

forma de comunicação por imagem e som, em tempo real, ao vivo, na linguagem da internet.

forma de comunicação digitada, em tempo real, em fora de bate-papo, na linguagem da internet.

Resolução

A nota média é calculada usando a seguinte fórmula:

nota média = $\displaystyle \frac{\text{soma das notas}}{\text{total de alunos}}$

Como sabemos que houve apenas 1 nota 10 e 9 notas 9, calculamos a soma das notas:

soma das notas = $1 \times 10 + 9 \times 9 = 91$

e como são 10 alunos, calculamos a média:

nota média = $ \displaystyle \frac{91}{10} $ = 9,1

Resposta: Alternativa (D)

Questão 2

Marcos e Alice encomendaram um bolo para comemorar o aniversário de sua mãe. Marcos pagou R$ 42,00, o que corresponde a 56% do preço do bolo, e o restante foi pago por Alice.

Qual foi o valor pago por Alice?

(A) R$ 27,00

(B) R$ 42,00

(D) R$ 75,00

(E) R$ 51,13

Resolução

Aqui basta usarmos uma regra de três. Se marcos pagou por 56% do bolo, então Alice deve ter pago os 44% restantes do bolo.

$ \begin{equation} 56 \% \propto \text{42,00} \\ 44 \% \propto x \end{equation} $

$ x = \displaystyle \frac{44 \times \text{42,00}}{56} $ = 33,00

Resposta: Alternativa (C)

Questão 3

Buscando manter a forma física, João e Pedro resolveram caminhar regularmente em torno de uma praça cujo formato é retagular. Enquanto João caminha 200 metros, Pedro caminha 100 metros. Ambos mantêm o mesmo ritmo de caminhada durante todo o trajeto. Partindo do mesmo ponto (A) ao mesmo tempo, em direções diferentes conforme indicação das setas na figura abaixo.

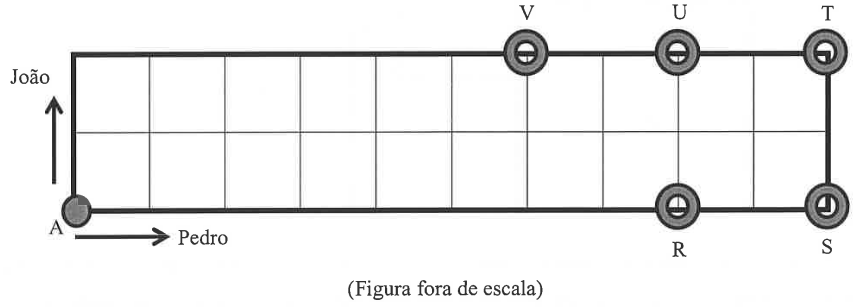
Na figura, a praça está dividida em 20 quadrados congruentes cujo perímetro de cada quadrado é 100 m. Em que ponto irão se encontrar pela primeira vez?

(A) V

(B) U

(D) S

(E) R

Resolução

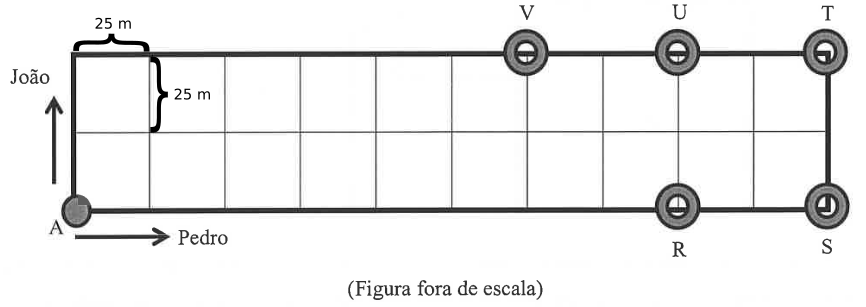
A primeira coisa a se fazer aqui é calcular quanto mede o lado de cada quadrado. Sendo o perímetro igual a 100 m, sabendo que no quadrado são 4 lados iguais, cada lado mede 25 m.

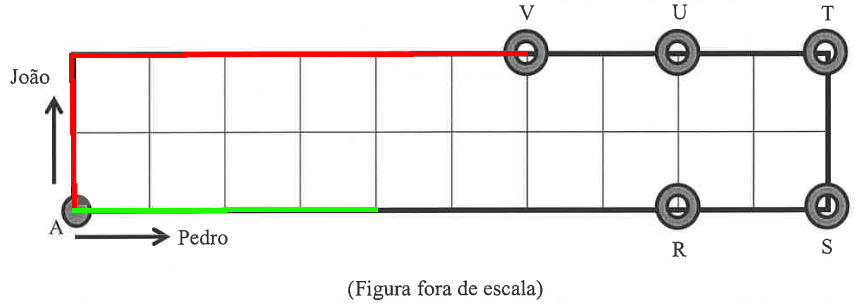
Logo, se João caminha 200 m, ele caminha por $ 200 \div 25 = 8 $ lados de quadrado, enquanto que Pedro caminha $ 100 \div 25 = 4 $ lados de quadrado. Podemos marcar na própria figura esses passos e assim encontrar visualmente a resposta:

Numa primeira rodada, João andou 8 lados, ou seja, 2 para cima mais 6 para a direita, enquanto Pedro andou 4 lados para a direita:

Numa próxima rodada, João andou mais 8 lados, ou seja, 4 para a direita, 2 para baixo e 2 para a esquerda, e Pedro andou mais 4 lados para a direita:

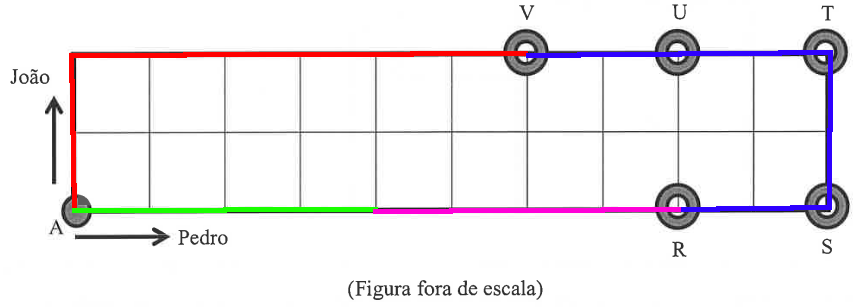
Assim, o primeiro encontro deles deu-se no ponto R.

Resposta: Alternativa (E)

Questão 4

Marcos está brincando com peças de madeira no formato de quadrados. Em um dado momento, organizou 5 (cinco) quadrados conforme a figura a seguir.

Considere que as peças estejam perfeitamente alinhadas, isso é, não existem espaços entre elas. Sabendo que os perímetros dos quadrados A, B e C são 20 cm, 2 dm e 0,48 m respectivamente, qual a área do quadrado E?

(A) 841 cm²

(B) 576 cm²

(D) 625 cm²

(E) 1156 cm²

Resolução

Como as respostas estão em cm², vamos primeiro calcular os lados dos quadrados em cm. Chamemos de a, b, c, d e e os lados respectivos aos quadrados A, B, C, D e E:

A: perímetro 20 cm, $a = 20 \div 4 = 5 $ cm

B: perímetro 2 dm = 20 cm, $b = 20 \div 4 = 5$ cm

C: perímetro 0,48 m = 48 cm, $c = 48 \div 4 = 12$ cm

D: visualmente, observamos que o lado do quadrado D é igual à soma dos lados dos quadrados B e C, ou seja, $d = b + c = 5 + 12 = 17$ cm

E: visualmente, observamos que a soma dos lados dos quadrados A e E é igual à soma dos lados dos quadrados C e D:

$ \begin{align} a + e & = c + d \\ e & = c + d - a \\ e & = 12 + 17 - 5 \\ e & = 24 \text{ cm} \end{align} $

E assim, calculamos a área do quadrado E:

$\text{área do quadrado} = \text{lado}^2 = e^2 = 24^2 = 576 $ cm²

Resposta: Alternativa (B)

Questão 5

Na casa de Márcio, existem copos com três diferentes capacidades: um copo pequeno cuja capacidade é de 100 ml, um copo médio e um copo grande.

A capacidade de cada copo pequeno corresponde a $\displaystyle \frac{1}{3}$ da capacidade do copo médio.

O copo médio tem capacidade correspondente a $\displaystyle \frac{2}{5}$ do copo grande.

Estando o copo pequeno cheio de água, o copo médio cheio de água e o copo grande vazio, transferimos, sem perda, toda a água do copo pequeno e do copo médio para o copo grande.

Em relação ao copo grande, podemos afirmar que:

(A) transbordará, pois a capacidade do copo grande é menor que a soma das capacidades dos copos menores.

(B) terá $\displaystyle \frac{8}{15}$ da sua capacidade preenchida pela água.

(D) terá exatamente metade da sua capacidade preenchida pela água.

(E) terá $\displaystyle \frac{11}{15}$ da sua capacidade preenchida pela água.

Resolução

Chamemos de P, M e G as capacidades dos copos pequeno, médio e grande, respectivamente. Já sabemos que P = 100 ml

Foi dado que $P = \displaystyle \frac{M}{3}$, ou seja, $M = 3P = 3 \times 100 = 300$ ml.

Também foi dado que $M = \displaystyle \frac{2G}{5}$, ou seja, $G = \displaystyle \frac{5M}{2} = \displaystyle \frac{5 \times 300}{2} = 750 $ ml.

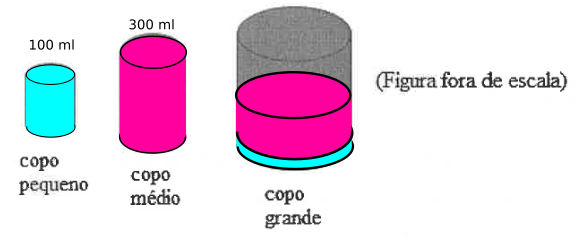
Ao despejar o conteúdo dos copos pequeno (100 ml) e médio (300 ml) no copo grande, não iremos enchê-lo, pois a soma deles é de 400 ml de água. Isso corresponde à fração de $ \displaystyle \frac{P+M}{G} = \displaystyle \frac{400}{750} = \displaystyle \frac{8}{15}$ da capacidade total do copo grande.

Resposta: Alternativa (B)

Questão 6

Arthur possui uma barraca de frutas e resolveu fazer uma promoção de laranjas conforme descrição abaixo:

Promoção 1: leve 6 e pague 5

Promoção 2: leve 10 e pague 8

Promoção 3: leve 20 e pague 18

Promoção 4: leve 27 e pague 24

Promoção 5: leve 35 e pague 30

João possui um restaurante e compra diariamente muitas laranjas, pois mesmo que não sejam consumidas no dia da compra, poderão ser armazenadas e consumidas nos dias seguintes.

Assinale abaixo qual das promoções seria mais vantajosa para João:

(A) promoção 1

(B) promoção 2

(D) promoção 4

(E) promoção 5

Resolução

Aqui precisamos descobrir qual das frações é a maior: $\displaystyle \frac{6}{5}$, $\displaystyle \frac{10}{8}$, $\displaystyle \frac{20}{18}$, $\displaystyle \frac{27}{24}$ ou $\displaystyle \frac{35}{30}$, pois quanto mais laranjas conseguimos levar em relação à quantidade paga, mais vantajosa é a promoção.

E para comparar frações de denominadores diferentes, precisamos reescrevê-las nas formas equivalentes com mesmo denominador e comparar os numeradores. Para isso, vamos calcular o MMC dos denominadores:

Vamos usar o dispositivo prático para encontrar o MMC

$ \begin{array}{c|c} 5,8,18,24,30 & 2 \\ \hline 5,4,9,12,15 & 2 \\ 5,2,9,6,15 & 2 \\ 5,1,9,3,15 & 2 \\ 5,1,3,1,5 & 2 \\ 5,1,1,1,5 & 2 \\ \hline 1,1,1,1,1 & 2³.3².5 = 360 \end{array} $

Agora, reescrevemos as promoções:

$ \displaystyle \frac{6}{5} \stackrel{\times 72}{=} \frac{432}{360} $
$ \displaystyle \frac{10}{8} \stackrel{\times 45}{=} \frac{450}{360} $
$ \displaystyle \frac{20}{18} \stackrel{\times 20}{=} \frac{400}{360} $
$ \displaystyle \frac{27}{24} \stackrel{\times 15}{=} \frac{405}{360} $
$ \displaystyle \frac{35}{30} \stackrel{\times 12}{=} \frac{420}{360} $

$ \displaystyle \frac{450}{360} > \displaystyle \frac{432}{360} > \displaystyle \frac{420}{360} > \displaystyle \frac{405}{360} > \displaystyle \frac{400}{360} $

Agora sim, podemos comparar as promoções e concluir que a melhor é a promoção 2

Resposta: Alternativa (B)

Questão 7 (ANULADA)

Miguel possui uma caixa que tem somente bolas vermelhas e bolas amarelas, sendo cada bola de uma única cor. Ele retira 12 bolas dessa caixa e, pelo menos uma delas, é da cor amarela. Em seguida, devolve as 12 bolas à caixa e retira, desta vez, 11 bolas, sendo que, pelo menos, duas delas são da cor vermelha. Miguel, então, devolve as 11 bolas à caixa. Por último, o menino retira, aleatoriamente, uma bola dessa caixa.

Qual a probabilidade dessa bola ser da cor vermelha?

(A) 55%

(B) 91,6%

(D) 60%

(E) 50%

Resolução

Com os dados da questão, não é possível calcular esta probabilidade. Mas vamos analizar os dados para ver até onde conseguimos chegar.

Antes de tudo, não sabemos quantas bolas tem no total dentro da caixa. Na primeira retirada, sabemos que a quantidade de bolas amarelas é pelo menos igual a 1, podendo ser mais. Na segunda retirada, sabemos que a quantidade de bolas vermelhas são 2, podendo ser mais também. E como na primeira retirada foram 12 bolas, também sabemos que temos no mínimo 12 bolas dentro da caixa.

A probabilidade de uma retirada ao acaso resultar numa bola vermelha é calculada por:

\[\text{probabilidade} = \frac{\text{quantidade de bolas vermelhas}}{\text{quantidade total de bolas}} \]

E não temos condições de descobrir nenhuma dessas quantidades. A questão foi provavelmente mal formulada ou mal adaptada.

Questão 8

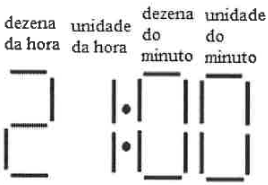
O display de um relógio digital que está situado na sala de aula do aluno João é formado por lâmpadas que podem ser ligadas ou desligadas de forma independente. Cada dígito pode ser composto por até 7 (sete) lâmpadas ligadas e o display é formado por 4 (quatro) blocos (dezena da hora, unidade da hora, dezena do minuto, unidade do minuto), conforme a figura 1.

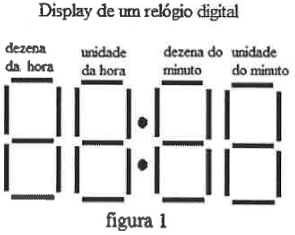
No entanto, o relógio dessa sala de aula está com defeito.

Nos quatro blocos, exatamente as mesmas duas lâmpadas de cada bloco queimaram e se mantém desligadas.

Considere que no exato momento em que João olha para o relógio, o horário mostrado é o da representação da figura 2:

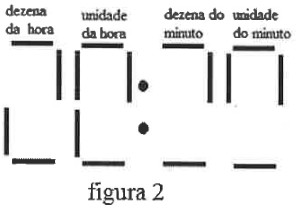
Com relação à figura 2, qual será a representação do relógio passados 21 (vinte e um) minutos após João tê-lo olhado?

(A)

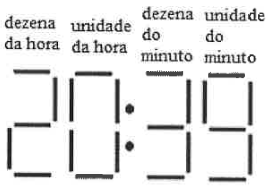
(B)

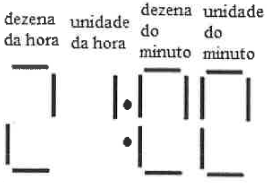
(C)

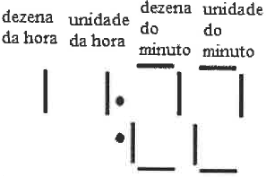
(D)

(E)

Resolução

Observando o dígito referente às dezenas de hora, sabendo que as horas vão de 00 até 23, poderíamos pensar que as 2 possibilidades são 2:

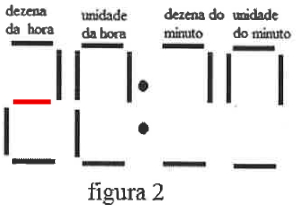
Ou 0 (zero):

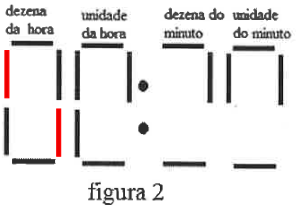
Porém, observando o dígito referente às unidades de hora, vemos que das 7 lâmpadas, 5 estão acesas. Assim, a única possibilidade é que as lâmpadas queimadas sejam a central e a inferior direita.

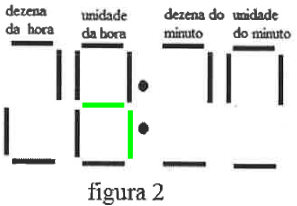
Com isso, voltando para as dezenas de hora, eliminamos a possibilidade de ser 0 (zero), pois a lâmpada superior esquerda precisaria estar acesa, mas não está. Sendo assim, a conclusão é que este dígito é o 2, ou seja, o dígito para unidades de horas só pode ser o 0, pois é o único valor que pode formar uma hora válida (20, 21, 22, 23), dadas as lâmpadas que já estão acesos.

Agora vamos pensar nos minutos. Nas dezenas só podemos ter o dígito 3, pois não tem como formar algo válido acendendo somente 1 das lâmpadas queimadas. E nas unidades só pode ser o dígito 9, pelos mesmos motivos.

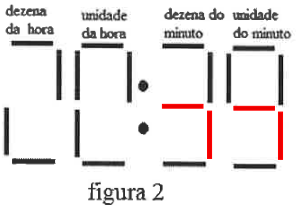
Assim, concluímos que quando João olha para o relógio são 20:39h, e quando se passam 21 minutos, chegamos a 21:00h, mas não podemos marcar a alternativa (B) por conta das lâmpadas queimadas, então temos que imaginar como seria a representação de 21:00h com os lâmpadas central e inferior direita apagadas.

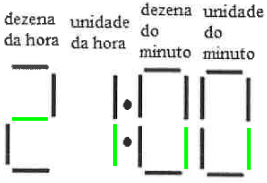
Resposta: Alternativa (C)

Questão 9

Marquinhos tem uma folha de cartolina no formato de retângulo com 60 cm x 40 cm e recortou, nos cantos, 4 quadradinhos de lado 4 cm, conforme indica a figura 1.

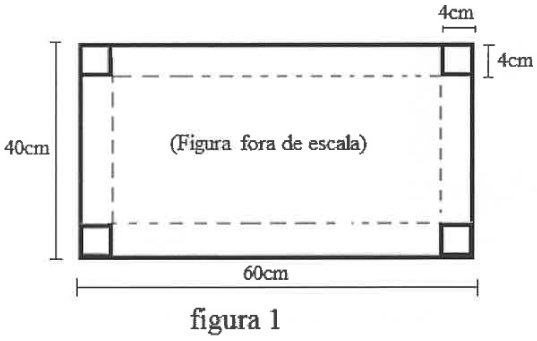
Posteriormente dobrou a cartolina nas linhas pontilhadas e construiu uma caixa em forma de paralelepípedo sem tampa conforme a figura 2.

Qual a capacidade da caixa correspondente à figura 2, em decímetros cúbicos?

(A) 6,656 dm³

(B) 16,64 dm³

(D) 66,56 dm³

(E) 665,6 dm³

Resolução

A base do paralelepípedo possui lados iguais a 52 cm (60 cm - 8 cm) e 32 cm (40 cm - 8 cm), pois descontamos os lados dos quadrados removidos. A altura do paralelepípedo é, naturalmente, 4 cm.

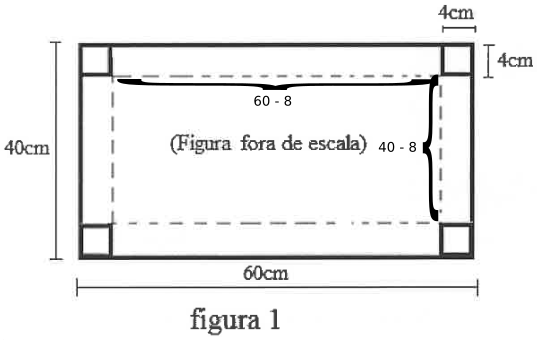
Convertendo em dm, as dimensões são 5,2 dm, 3,2 dm e 0,4 dm. E o volume é calculado pelo produto destes 3 valores:

$ \text{volume do paralelepípedo} = \text{5,2} \times \text{3,2} \times{0,4} = \text{6,656}$ dm³

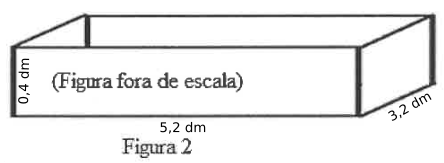
Resposta: Alternativa (A)

Questão 10

Em virtude da quarentena e com as aulas suspensas, Carlos comprou uma grande quantidade de bolinhas de gude para que seu filho João pudesse brincar no quintal de casa.

João ordenou as bolinhas de gude representando quadrados conforme as figuras abaixo.

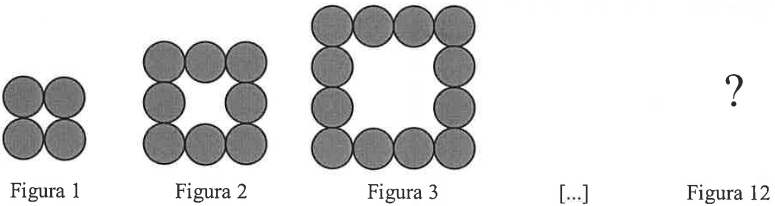
Supondo que João mantenha o padrão, quantas bolinhas ele irá utilizar para construir a figura 12?

(A) 169

(B) 121

(D) 44

(E) 52

Resolução

É possível encontrar uma lei de formação neste padrão. Observe que na Figura 1, temos um quadrado 2x2. Na Figura 2, temos um quadrado 3x3, descontando um quadrado 1x1. Na Figura 3, temos um quadrado 4x4 descontando um quadrado 2x2. Podems reescrever essas relações como:

Figura 1: (1+1)x(1+1) - 0 = (1+1)x(1+1) - (1-1)x(1-1)

Figura 2: (2+1)x(2+1) - (1)x(1) = (2+1)x(2+1) - (2-1)x(2-1)

Figura 3: (3+1)x(3+1) - (2)x(2) = (3+1)x(3+1) - (3-1)x(3-1)

Agora sim, temos um padrão. Para a Figura N, teremos (N+1)x(N+1) - (N-1)x(N-1) bolinhas. Para o caso da figura 12, são (12+1)x(12+1) - (12-1)x(12-1) = 13x13 - 11x11 = 169 - 121 = 48 bolinhas.

Resposta: Alternativa (C)

Questão 11

Vinícius resolveu criar uma estratégia de treinamento para participar da Maratona de Curitiba cujo percurso é de 42.195 m. A cada semana, ele corre 650 m a mais do que na semana anterior. Nesse ritmo ele correu na vigésima oitava semana 23.750 m.

Considerando as informações acima, pode-se estimar que faltam quantas semanas para Vinícius ultrapassar pela primeira vez a medida da Maratona de Curitiba?

(A) 20 semanas

(B) 24 semanas

(D) 29 semanas

(E) 32 semanas

Resolução

Como a cada semana existe um acréscimo de 650 m em relação à semana anterior, podemos dizer que as quantidade de metros em relação ao número da semana formam uma Progressão Aritmética (P.A.). Na P.A., o termo geral $a_n$ é calculado por: \[a_n = a_1 + (n-1) \cdot r\] Sendo $a_1$ o primeiro termo, que no caso seria a quantidade de metros da 1ª semana, $n$ é o número da semana e $r$ a razão, ou seja, 650. Vamos calcular $a_1$: \[a_1 = a_{28} - (28-1) \cdot r = 23750 - 27 \cdot 650 = 23750 - 17550 = 6200\] OK, sabendo que na primeira semana ele percorrei 6200 metros, podemos calcular qual será a semana $k$ que ultrapassará o valor de 42195:

\[ a_1 + (k-1) \cdot r > 42195 \\ 6200 + (k-1) \cdot 650 > 42195 \\ (k-1) \cdot 650 > 42195 - 6200 \\ k-1 > \frac{35995}{650} \\ k > 1 + \text{55,37} \\ k > \text{56,37} \] O menor valor possível inteiro de k é 57. Se estamos na 28ª semana, faltam 29 semanas.

Resposta: Alternativa (D)

Questão 12

Thaíssa recebeu a conta de água do mẽs de setembro de 2020 da sua residência, na qual o consumo foi de 26 (vinte e seis) m³ e o custo da fatura foi detalhado da seguinte forma:

10 x R$ 1,50 + 10 x R$ 2,80 + 6 x R$ 4,80 = R$ 71,80

O serviço é cobrado por faixas de consumo, de acordo com a tabela abaixo:

\[ \begin{array}{|c|c|} \hline \text{Consumo} & \text{Custo por metro cúbico} \\ \hline \text{Até 10 m³} & \text{R\$ 1,50} \\ \hline \text{Acima de 10 m³} & \text{R\$ 2,80} \\ \text{e até 20 m³} & \\ \hline \text{Acima de 20 m³} & \text{R\$ 4,80} \\ \hline \end{array} \]

Considerando os valores da tabela acima, de quanto seria o valor da conta de água de Thaíssa do mês de setembro de 2020 se o consumo tivesse sido de 30 m³?

(A) R$ 76,40

(B) R$ 80,40

(D) R$ 85,80

(E) R$ 91,00

Resolução

Olhando para o detalhamento da fatura, conclui-se que Thaíssa consumiu 26 m³ neste mês. Se tivesse consumido 30 m³, ou seja, 4 m³ a mais, estes 4 m³ seriam cobrados R$ 4,80 por m³, por estar na faixa acima de 20 m³. Logo a conta seria de 4 x R$ 4,80 = R$ 19,20 a mais.

R$ 71,80 + R$ 19,20 = R$ 91,00.

Resposta: Alternativa (E)

2019/2020

Esta prova pode ser baixada em https://www.concursosmilitares.com.br/provas-anteriores/exercito/colegio-militar/curitiba/cmc-2019-2020-matematica-fundamental.pdf

O gabarito oficial pode ser baixado em https://www.concursosmilitares.com.br/provas-anteriores/exercito/colegio-militar/curitiba/cmc-2019-2020-gabarito-fundamental.pdf

Porém estou disponibilizando a prova aqui caso tenha algum problema de acesso no link original e o gabarito aqui

Questão 1

Ao ingressar em um Colégio Militar, cada aluno escolhe um único grêmio estudantil para fazer parte. No ano de 2019, os 900 alunos matriculados no Colégio Militar de Curitiba (CMC) escolheram entre os grêmios da Infantaria, da Cavalaria, da Artilharia, da Intendência e da Banda. Além disso, o colégio organiza os alunos em três companhias (Cia). Os 200 alunos de 6º e 7º anos compõem a 3ª Cia; os 300 alunos de 8º e 9º anos compõem a 2ª Cia e os 400 alunos do Ensino Médio compõem a 1ª Cia. O gráfico abaixo apresenta a quantidade de alunos de cada uma das companhias distribuídos nos cinco diferentes grêmios estudantis do CMC no ano de 2019.

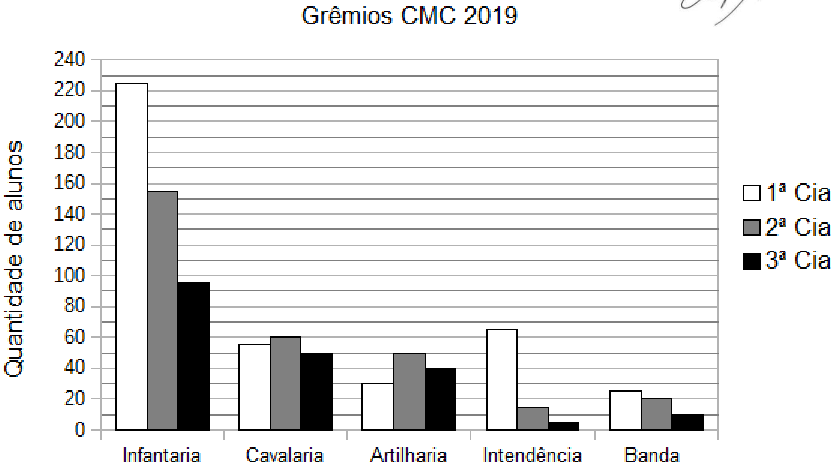
Com base nas informações fornecidas é correto afirmar que:

(A) a maioria dos alunos da 2ª Cia escolheu o grêmio da Cavalaria.

(B) o grêmio da Intendência tem mais componentes que o grêmio da Artilharia.

(D) na 3ª Cia, a Banda possui menos integrantes do que o grêmio da Intendência.

(E) há mais alunos da 1ª Cia no grêmio da Intendência do que o total de alunos da Banda.

Resolução

Esta é uma questão de interpretação de gráficos. É preciso ler as alternativas e verificar se ela é verdadeira ou falsa.

Uma forma de organizar os dados é colocar em forma de tabela. Como existem alternativas que comparam grêmios inteiros ou Cias inteiras, vamos calcular os totais também:

$ \begin{array}{|c|c|c|c|c|c|c|} \hline & \text{Infantaria} & \text{Cavalaria} & \text{Artilharia} & \text{Intendência} & \text{Banda} & \text{Total da Cia}\\ \hline \text{1ª Cia} & 225 & 55 & 30 & 65 & 25 & 400 \\ \text{2ª Cia} & 155 & 60 & 50 & 35 & 20 & 320 \\ \text{3ª Cia} & 95 & 50 & 40 & 5 & 10 & 200 \\ \hline \text{Total do Grêmio} & 505 & 165 & 120 & 105 & 55 & \\ \hline \end{array} $

Vamos avaliar cada uma das alternativas:

Alternativa (A): Ao observar somente os dados da 2ª Cia, é fácil notar que o grêmio mais escolhido é o da Infantaria, com 155 alunos. A Cavalaria é o segundo mais escolhido, com 60 alunos, logo esta alternativa é falsa. $ \begin{array}{|c|c|c|c|c|c|c|} \hline & \text{Infantaria} & \text{Cavalaria} & \text{Artilharia} & \text{Intendência} & \text{Banda} & \text{Total da Cia}\\ \hline \text{1ª Cia} & 225 & 55 & 30 & 65 & 25 & 400 \\ \text{2ª Cia} & \fbox{155} & \fbox{60} & 50 & 35 & 20 & 320 \\ \text{3ª Cia} & 95 & 50 & 40 & 5 & 10 & 200 \\ \hline \text{Total do Grêmio} & 505 & 165 & 120 & 105 & 55 & \\ \hline \end{array} $

Alternativa (B): Comparando os totais da Intendência (105) com da Artilharia (120), também concluímos que esta alternativa é falsa. $ \begin{array}{|c|c|c|c|c|c|c|} \hline & \text{Infantaria} & \text{Cavalaria} & \text{Artilharia} & \text{Intendência} & \text{Banda} & \text{Total da Cia}\\ \hline \text{1ª Cia} & 225 & 55 & 30 & 65 & 25 & 400 \\ \text{2ª Cia} & 155 & 60 & 50 & 35 & 20 & 320 \\ \text{3ª Cia} & 95 & 50 & 40 & 5 & 10 & 200 \\ \hline \text{Total do Grêmio} & 505 & 165 & \fbox{120} & \fbox{105} & 55 & \\ \hline \end{array} $

Alternativa (C): O grêmio da Infantaria possui 225 alunos da 1ª Cia, e somando os alunos da 2ª Cia (155) com a 3ª Cia (95), temos 250 alunos, então esta alternativa também é falsa. $ \begin{array}{|c|c|c|c|c|c|c|} \hline & \text{Infantaria} & \text{Cavalaria} & \text{Artilharia} & \text{Intendência} & \text{Banda} & \text{Total da Cia}\\ \hline \text{1ª Cia} & \fbox{225} & 55 & 30 & 65 & 25 & 400 \\ \text{2ª Cia} & \fbox{155} & 60 & 50 & 35 & 20 & 320 \\ \text{3ª Cia} & \fbox{95} & 50 & 40 & 5 & 10 & 200 \\ \hline \text{Total do Grêmio} & 505 & 165 & 120 & 105 & 55 & \\ \hline \end{array} $

Alternativa (D): Na 3ª Cia, são 10 alunos na Banda e 5 alunos na Intendência, logo, falsa também. $ \begin{array}{|c|c|c|c|c|c|c|} \hline & \text{Infantaria} & \text{Cavalaria} & \text{Artilharia} & \text{Intendência} & \text{Banda} & \text{Total da Cia}\\ \hline \text{1ª Cia} & 225 & 55 & 30 & 65 & 25 & 400 \\ \text{2ª Cia} & 155 & 60 & 50 & 35 & 20 & 320 \\ \text{3ª Cia} & 95 & 50 & 40 & \fbox{5} & \fbox{10} & 200 \\ \hline \text{Total do Grêmio} & 505 & 165 & 120 & 105 & 55 & \\ \hline \end{array} $

Alternativa (E): Como as anteriores são falsas, só restou esta como verdadeira, certo? Mas é bom conferir. Os alunos da Intendência da 1ª Cia são 65. O total da Banda é 55, então esta alternativa é verdadeira mesmo. $ \begin{array}{|c|c|c|c|c|c|c|} \hline & \text{Infantaria} & \text{Cavalaria} & \text{Artilharia} & \text{Intendência} & \text{Banda} & \text{Total da Cia}\\ \hline \text{1ª Cia} & 225 & 55 & 30 & \fbox{65} & 25 & 400 \\ \text{2ª Cia} & 155 & 60 & 50 & 35 & 20 & 320 \\ \text{3ª Cia} & 95 & 50 & 40 & 5 & 10 & 200 \\ \hline \text{Total do Grêmio} & 505 & 165 & 120 & 105 & \fbox{55} & \\ \hline \end{array} $

Resposta: Alternativa (E)

Questão 2

Maria Fernanda foi a uma lanchonete para fazer um lanche. Chegando lá, quando pegou o cardápio, percebeu que havia algumas informações apagadas, como mostra a figura a seguir, na qual para cada produto é apresentado o seu respectivo valor unitário.

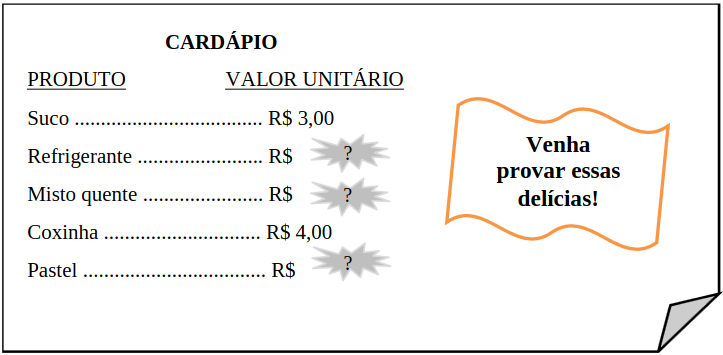
Enquanto esperava para fazer seu pedido, Maria Fernanda verificou que três pessoas foram ao caixa para pagar suas contas. A primeira delas consumiu dois mistos quentes e um suco, gastando, ao todo, R$ 17,00. A segunda pessoa consumiu um refrigerante e dois pastéis, gastando, ao todo, R$ 17,00. Já a terceira consumiu um refrigerante, uma coxinha e um misto quente, gastando, ao todo, R$ 16,00. Maria Fernanda, então, fez o seu lanche, tomando um refrigerante e comendo um misto quente e dois pastéis.

Qual o valor pago por Maria Fernanda pelo lanche?

(A) R$ 20,00

(B) R$ 24,00

(D) R$ 28,00

(E) R$ 25,00

Resolução

Existem 3 valores que não conhecemos, os preços do Refrigerante (R), do Misto Quente (M) e do Pastel (P). Podemos usar as informações dadas para escrever equações envolvendo essas quantidades desconhecidas:

"A primeira delas consumiu dois mistos quentes e um suco, gastando, ao todo, R$ 17,00":

$ 2 \times M + \text{Suco} = 17 $

Aqui usamos o valor conhecido do Suco (R$ 3,00). Vamos resolver para achar M:

$ \begin{align} 2 \times M + 3 &= 17 \\ 2 \times M &= 17 - 3 \\ 2 \times M &= 14 \\ M &= \displaystyle \frac{14}{2} \\ M &= 7 \end{align}
$

E encontramos o preço do Misto Quente: R$ 7,00. Vamos ver outras informações:

"A segunda pessoa consumiu um refrigerante e dois pastéis, gastando, ao todo, R$ 17,00"

$ R + 2 \times P = 17 $

Como não sabemos os valores de R nem P, é melhor vermos o que tem na próxima:

"Já a terceira consumiu um refrigerante, uma coxinha e um misto quente, gastando, ao todo, R$ 16,00"

$ R + \text{Coxinha} + \text{Misto Quente} = 16 $

OK, aqui já usamos o valor conhecido da Coxinha (R$ 4,00) e o valor calculado do Misto Quente (R$ 7,00):

$ \begin{align} R + 4 + 7 &= 16 \\ R + 11 &= 16 \\ R &= 16 - 11 \\ R &= 5 \end{align} $

Muito bem, calculamos aqui que o Refrigerante custa R$ 5,00, e podemos retornar na equação anterior:

$ \begin{align} R + 2 \times P &= 17 \\ 5 + 2 \times P &= 17 \\ 2 \times P &= 17 - 5 \\ 2 \times P &= 12 \\ P &= \displaystyle \frac{12}{2} \\ P &= 6 \end{align}
$

Pronto, achamos o preço do Pastel, R$ 6,00.

A questão pede o valor da conta da Maria Fernanda, que consumiu 1 Refrigerante, 1 Misto Quente e 2 Pastéis:

$ \begin{equation} R + M + 2 \times P\\ = 5 + 7 + 2 \times 6\\ = 12 + 12\\ = 24 \end{equation}
$

Resposta: Alternativa (B)

Questão 3

A tabela a seguir mostra a lista dos oito países mais populosos do mundo no ano de 2018.

\[ \begin{array}{|c|c|c|} \hline \text{Classificação} & \text{País} & \text{População (em número de habitantes)} \\ \hline 1º & \text{China} & 1.384.688.986 \\ \hline 2º & \text{Índia} & 1.296.834.042 \\ \hline 3º & \text{Estados Unidos} & 329.145.465 \\ \hline 4º & \text{Indonésia} & 262.787.403 \\ \hline 5º & \text{Brasil} & 208.846.892 \\ \hline 6º & \text{Paquistão} & 207.862.518 \\ \hline 7º & \text{Nigéria} & 195.300.340 \\ \hline 8º & \text{Bangladesh} & 159.453.001 \\ \hline \end{array} \]

_{^{Disponível em: https://epocanegocios.globo.com/Mundo/noticia/2017/12/estes-serao-os-paises-mais-populosos-de-2018.html Acesso: 23 de Julho de 2019.}}

De acordo com os dados apresentados, pode-se afirmar que a diferença entre a soma da população dos dois países mais populosos e a soma do 5º e do 7º países da lista é um número que possui:

(A) 10 ordens, 4 classes e o algarismo das dezenas é 7.

(B) 4 ordens, 10 classes e o algarismo das dezenas é 9.

(D) 10 ordens, 4 classes e o algarismo das centenas de milhão é 2.

(E) 10 ordens, 4 classes e algarismo das unidades de milhão é 3.

Resolução

Aqui é preciso interpretar o que foi pedido. "a diferença entre a soma da população dos dois países mais populosos e a soma do 5º e do 7º países" quer dizer que precisamos primeiro somar as populações dos 1º e 2º países da lista e subtrair a soma das populações do 5º e 7º:

$ (1º + 2º) - (5º + 7º) \\ = (1.384.688.986 + 1.296.834.042) - (208.846.892 + 195.300.340) \\ = 2.681.523.028 - 404.147.232 \\ = 2.277.375.796 $

É um número de 10 algarismos, logo 10 ordens. Foi necessário separar em 4 grupos de até 3 algarismos, logo 4 classes. Assim já eliminamos as alternativas (B) e (C), e temos que avaliar as demais alternativas:

Alternativa (A): O algarismo das dezenas de 2.277.375.796 é o 9, logo, falsa.

Alternativa (D): O algarismo das dezenas de milhão de 2.277.375.796 é o 7, logo, verdadeira. Mas vamos ver o que diz a próxima também.

Alternativa (E): O algarismo das unidades de milhão de 2.277.375.796 é o 7, logo, falsa.

Resposta: Alternativa (D)

Questão 4

Maria Victoria pretende comprar uma mala de viagem em formato de cubo ou paralelepípedo para transportar como bagagem de mão em uma viagem aérea. Como a garota deve respeitar as normas da companhia aérea, que estabelecem que a soma das medidas (comprimento + largura + altura) da bagagem de mão não deve ser maior que 115 cm, sua escolha deve ser bastante cuidadosa. Observe a seguir algumas opções de malas apresentadas à Maria Victoria por uma loja:

I - uma mala em formato cúbico com arestas medindo 0,45 m;

II - uma mala em formato de paralelepípedo com 2,5 dm de largura, 350 mm de comprimento, e 0,55 m de altura;

III - uma mala em formato cúbico com arestas medindo 390 mm; e

IV - uma mala em formato de paralelepípedo com 4,8 dm de altura, largura 25% menor que a altura e comprimento 25% menor que a largura.

A(s) opção(ões) de mala que Maria Victoria deve escolher, atendendo às normas estabelecidas pela companhia aérea para levar como bagagem de mão, é(são) somente o(s) modelo(s):

(A) II e III.

(B) I, II e III.

(D) II e IV.

(E) II.

Resolução

Como a regra da soma das dimensões foi dada em cm, vamos convertendo tudo em cm para depois fazer as somas.

I - Cubo de 0,45 m de aresta: 3 lados iguais de 45 cm, logo $3 \times 45 = 135$ cm. Como 135 > 115, Maria não pode usar este modelo. Já podemos eliminar a alternativa (B).

II - 2,5 dm = 25 cm; 350 mm = 35 cm; 0,55 m = 55 cm. $25 + 35 + 55 = 115$ cm. Este modelo tem a medida exatamente no limite do permitido. Assim, eliminamos também a alternativa (C), que não contém o modelo II como opção.

III - 390 mm = 39 cm. Sendo um cubo, a soma das medidas é $ 3 \times 39 = 117 $ cm. Este modelo também não pode, e eliminamos a alternativa (A).

IV - A altura é de 4,8 dm = 48 cm. A largura, sendo 25% menor, precisa medir 75% de 48 cm.

$ \begin{align} 100\% & \propto 48 \\ 75\% & \propto L \\ \end{align} $

$ L = \displaystyle \frac{75 \times 48}{100} = \displaystyle \frac{3600}{100} = 36 $

OK, a largura mede 36 cm. A altura é 25% da largura, logo, regra de três novamente:

$ \begin{align} 100\% & \propto 36 \\ 75\% & \propto A \\ \end{align} $

$ A = \displaystyle \frac{75 \times 36}{100} = \displaystyle \frac{2700}{100} = 27 $

Pronto, temos as três dimensões do modelo IV. $48 + 36 + 27 = 111$ cm, então também pode-se usar este modelo.

Resposta: Alternativa (D)

Questão 5

José Augusto, um agricultor que preza pelas tradições, resolveu preparar um terreno para o plantio utilizando como medida o litro. Isso mesmo! Os antigos utilizavam o litro como uma forma de associar a área necessária para plantar a quantidade de sementes que enchessem completamente um recipiente com capacidade de um litro. Utilizando a ideia citada, o agricultor pretende plantar feijão num terreno retangular com 120 m de largura e com comprimento igual a $\displaystyle \frac{3}{10}$ da medida da largura. Para fins de cálculo, José Augusto sabe que exatamente 3.270 grãos de feijão cabem em um recipiente com 1 litro de capacidade quando totalmente cheio, e que essa quantidade de grãos de feijão plantada cobre uma área de 600 m².

Assim, para realizar o plantio do feijão em todo o seu terreno, José precisará exatamente de:

(A) 23.544 grãos de feijão.

(B) 1.046 grãos de feijão.

(D) 10.460 grãos de feijão.

(E) 2.354 grãos de feijão.

Resolução

Primeiro vamos calcular o comprimento:

$ \begin{equation} \text{Comprimento} = \displaystyle \frac{3}{10} \times \text{Largura} \\ \text{Comprimento} = \displaystyle \frac{3}{10} \times 120 = \displaystyle \frac{3 \times 120}{10} = \frac{360}{10} = 36 \\ \end{equation} $

Agora calculamos a área do terreno de José:

$ \begin{equation} \text{Area} = \text{Comprimento} \times \text{Largura} \\ \text{Area} = 36 \times 120 = 4.320 \text{m²}\\ \end{equation} $

E podemos calcular quantos grãos caberão nesta área:

$ \begin{align} 600 \text{ m²} &\propto 3.270 \text{ feijões} \\ 4.320 \text{ m²} &\propto x \text{ feijões} \end{align} $

$ x = \displaystyle \frac{4.320 \times 3.270}{600} = \displaystyle \frac{14.126.400}{600} = 23.544 $

Resposta: Alternativa (A)

Questão 6

Na malha quadriculada de 15x15 quadradinhos, ilustrada abaixo, está desenhada uma figura construída a partir das sete peças de um Tangram e identificadas cada uma com uma letra.

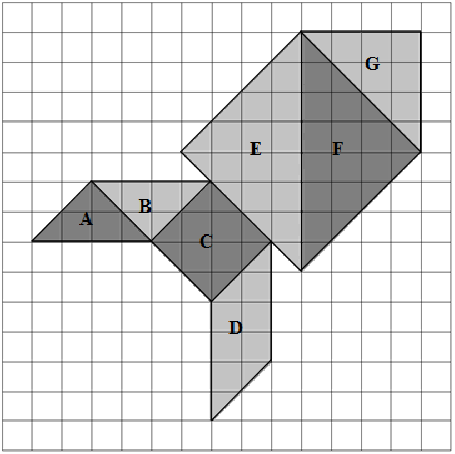
Considere que todos os quadradinhos da malha quadriculada possuem a mesma área. Observe as áreas identificadas na figura e considere as afirmações a seguir:

I - A área de F é igual à soma das áreas de A, de B e de G.

II - A área de C é 50% da área de E.

III - A área de D é 50% da soma das áreas de E e de A.

IV - A soma das áreas de E e de F é igual à soma das áreas de A, de B, de C e de D.

V - A soma das áreas de D e de A é igual à área de G.

VI - A área de G é igual à soma das áreas de A e de B.

São verdadeiras somente as afirmações:

(A) I, II, V e VI.

(B) I, II e VI.

(D) II, III e IV.

(E) II, V e VI.

Resolução

Para resolver, é preciso conhecer as formas de calcular áreas de quadriláteros e triângulos.

Quadriláteros: $ \text{Área} = \text{base} \times \text{altura} $

Triângulos: $ \text{Área} = \displaystyle \frac{\text{base} \times \text{altura}}{2}$

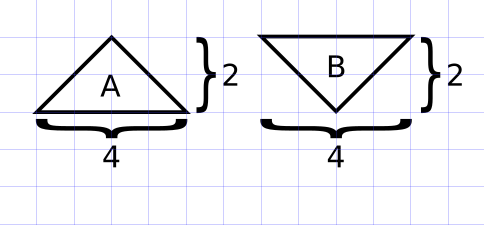
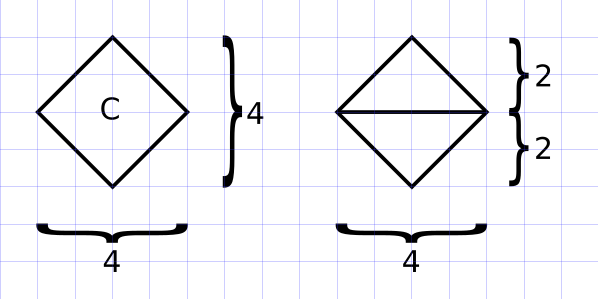
Agora, vamos às figuras. Os triângulos A e B são congruentes, de base 4 e altura 2. Assim, a área de ambos é igual a $ \displaystyle \frac{4 \times 2}{2} = 4$.

O quadrado C pode ser dividido em 2 triângulos de base 4 e altura 2, logo a área é igual a $ 2 \times \displaystyle \frac{4 \times 2}{2} = 2 \times 4 = 8$.

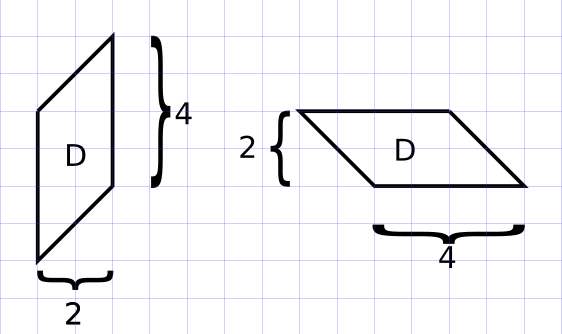
O paralelogramo D possui base 4 e altura 2, logo área igual a $4 \times 2 = 8$.

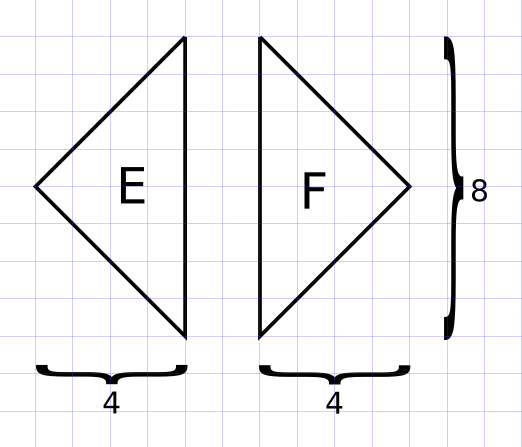
Os triângulos E e F são congruentes, de base 8 e altura 4, logo área igual a $ \displaystyle\frac{8 \times 4}{2} = 16 $.

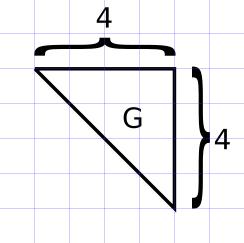
O triângulo G tem base 4 e altura 4, logo área igual a $ \displaystyle \frac{4 \times 4}{2} = 8 $.

Também podemos tabelar esses valores para avaliar mais facilmente as afirmações:

$ \begin{array}{|c|c|c|c|c|c|c|} \hline A & B & C & D & E & F & G \\ \hline 4 & 4 & 8 & 8 & 16 & 16 & 8 \\ \hline \end{array} $

"I - A área de F é igual à soma das áreas de A, de B e de G." - Verdadeira (16 = 4 + 4 + 8)

"II - A área de C é 50% da área de E." - Verdadeira (8 = 50% de 16)

"III - A área de D é 50% da soma das áreas de E e de A." - Falsa (A + E = 4 + 16 = 20, e 50% de 20 é 10, e não 8)

"IV - A soma das áreas de E e de F é igual à soma das áreas de A, de B, de C e de D." - Falsa (E + F = 16 + 16 = 32. A + B + C = 4 + 4 + 8 = 16).

"V - A soma das áreas de D e de A é igual à área de G." - Falsa (D + A = 8 + 4 = 12, e G = 8)

"VI - A área de G é igual à soma das áreas de A e de B." - Verdadeira (8 = 4 + 4)

Resposta: Alternativa (B)

Questão 7

Imaginemos que cada cidadão brasileiro consome, em média, dois copos e meio de leite por dia, enquanto um cidadão estrangeiro consome, em média, apenas meio copo de leite por dia. Considere duas famílias, uma brasileira e a outra estrangeira, cada uma delas com cinco integrantes, e todos eles seguindo o padrão citado.

Se o copo adotado como medida tem 275 ml de capacidade, pode-se afirmar que uma família brasileira, em um período de 15 dias, consome, em média:

(A) 41,25 l de leite a mais que uma família estrangeira.

(B) 4.125 dl de leite a mais que uma família estrangeira.

(D) 4,125 l de leite a mais que uma família estrangeira.

(E) 41,15 ml de leite a mais que uma família estrangeira.

Resolução

Vamos calcular quanto de leite cada família consome em 15 dias:

Brasileira: 5 integrantes x 2,5 copos por integrante x 275 ml por copo x 15 dias = 5 x 2,5 x 275 = 51.562,5 ml de leite

Estrangeira: 5 integrantes x 0,5 copo por integrante x 275 ml por copo x 15 dias = 5 x 0,5 x 275 = 10.312,5 ml de leite

Diferença: 51.562,5 - 10.312,5 = 41.250 ml

Não existe esta opção nas alternativas, mas como 1.000 ml = 1 l, então a diferença fica 41,25 l de leite.

Resposta: Alternativa (A)

Questão 8

Cinco amigos – Júlio, Eliana, Melissa, Rafael e Lucas – resolveram formar uma fila em ordem de altura.

Sabe-se que:

– Rafael é mais alto do que Eliana e do que Melissa;

– Lucas é mais alto do que Melissa;

– Júlio é mais baixo do que Rafael e do que Lucas;

– Eliana não é a mais baixa dos cinco amigos;

– Júlio é mais alto do que Eliana; e

– Lucas não é o mais alto dos cinco.

Considerando as informações anteriores, a ordem de altura decrescente dos amigos na fila é:

(A) Melissa, Eliana, Júlio, Lucas e Rafael.

(B) Lucas, Rafael, Júlio, Eliana e Melissa.

(D) Rafael, Eliana, Júlio, Lucas e Melissa.

(E) Júlio, Eliana, Lucas, Rafael e Melissa.

Resolução

Aqui é mais fácil olhar para as alternativas e ir eliminando as que quebram alguma regra.

"Rafael é mais alto do que Eliana e do que Melissa": Aqui eliminamos a alternativa (A), que coloca Rafael como o mais baixo de todos, e a alternativa (E), que coloca Rafael mais baixo que Eliana.

~~(A)~~ (B) (C) (D) ~~(E)~~

"Lucas é mais alto do que Melissa": Olhando só para as alternativas (B), (C) e (D), vamos que nenhuma delas pode ser eliminada, pois colocam Melissa como a mais baixa de todas.

~~(A)~~ (B) (C) (D) ~~(E)~~

"Júlio é mais baixo do que Rafael e do que Lucas": Novamente, só (B), (C) e (D): Aqui podemos eliminar a alternativa (D) porque coloca Júlio mais alto que Lucas.

~~(A)~~ (B) (C) ~~(D)~~ ~~(E)~~

"Eliana não é a mais baixa dos cinco amigos": Esta regra não nos ajuda em nada. Eliana não é a última em nenhuma das alternativas.

~~(A)~~ (B) (C) ~~(D)~~ ~~(E)~~

"Júlio é mais alto do que Eliana": Nas 2 alternativas que restaram, Júlio está mais à esquerda de Eliana, então continuamos com ambas válidas.

~~(A)~~ (B) (C) ~~(D)~~ ~~(E)~~

"Lucas não é o mais alto dos cinco": Aqui podemos eliminar a alternativa (B), pois esta coloca Lucas como o mais alto. E assim, só restou uma alternativa válida.

~~(A)~~ ~~(B)~~ (C) ~~(D)~~ ~~(E)~~

Resposta: Alternativa (C)

Questão 9

Um renomado chefe de cozinha decidiu montar um novo prato de salada para acrescentar no cardápio de seu restaurante. Esse novo prato terá rúcula, alface, queijo minas, tomate cereja, ovo de codorna, palmito, vinagre balsâmico e azeite de oliva.

No mercado, o chefe encontrou os seguintes preços para os ingredientes:

– rúcula: R$ 3,64 cada maço;

– alface: R$ 2,40 cada maço;

– queijo minas: R$ 30,00 cada quilograma;

– tomate cereja: R$ 5,75 cada 300 g;

– ovo de codorna: R$ 3,00 cada dúzia;

– palmito: R$ 15,00 cada 300 g;

– vinagre balsâmico: R$ 40,00 cada 500 ml e

– azeite de oliva: R$ 30,00 cada 750 ml.

As porções de ingredientes serão feitas pelo chefe da seguinte forma:

– 1 maço de rúcula para 7 porções;

– 1 maço de alface para 6 porções;

– 500 g de queijo minas para 5 porções;

– 180 g de tomate cereja para 3 porções;

– meia dúzia de ovos de codorna para 2 porções;

– 300 g de palmito para 6 porções;

– 300 ml de vinagre balsâmico para 20 porções e

– 40 ml de azeite de oliva para 2 porções.

Com base nessas informações, qual será o custo dos ingredientes para um prato completo da salada, considerando-se que para a sua montagem é utilizada uma porção de cada ingrediente?

(A) R$ 10,27

(B) R$ 10,32

(D) R$ 10,65

(E) R$ 10,96

Resolução

$\require{cancel}$ Para cada ingrediente, vamos primeiro calcular a quantidade de ingrediente que vai em 1 porção e então calcular o custo desta fração de ingrediente para compor o preço do prato de salada.

Rúcula: 1 maço rende 7 porções, logo 1 porção utiliza $\displaystyle \frac{1}{7}$ de maço.

$ \begin{align} 1 \text{ maço} & \propto \text{3,64} \\ \displaystyle \frac{1}{7} \text{ maço} & \propto x \\ \end{align}\\ x = \displaystyle \frac{1}{7} \times \text{3,64} = \frac{\text{3,64}}{7} = \text{0,52} $

Alface: 1 maço rende 6 porções, logo 1 porção utiliza $\displaystyle \frac{1}{6}$ de maço.

$ \begin{align} 1 \text{ maço} & \propto \text{2,40} \\ \displaystyle \frac{1}{6} \text{ maço} & \propto x \\ \end{align}\\ x = \displaystyle \frac{1}{6} \times \text{2,40} = \frac{\text{2,40}}{6} = \text{0,40} $

Queijo minas: 500 g para 5 porções, logo 100 g para 1 porção. Lembrando que 1 kg = 1.000 g.

$ \begin{align} 1.000 \text{ g} & \propto \text{30,00} \\ 100 \text{ g} & \propto x \\ \end{align}\\ x = \displaystyle \frac{\cancelto{1}{100} \times \text{30,00}}{\cancelto{10}{1.000}} = \frac{\text{30,00}}{10} = \text{3,00} $

Tomate cereja: 180 g para 3 porções, logo 60 g para 1 porção.

$ \begin{align} 300 \text{ g} & \propto \text{5,75} \\ 60 \text{ g} & \propto x \\ \end{align}\\ x = \displaystyle \frac{\cancelto{1}{60} \times \text{5,75}}{\cancelto{5}{300}} = \frac{5,75}{5} = \text{1,15} $

Ovos de codorna: meia dúzia de ovos (6 ovos) para 2 porções, logo 3 ovos para 1 porção.

$ \begin{align} 12 & \propto \text{3,00} \\ 3 & \propto x \\ \end{align}\\ x = \displaystyle \frac{\cancelto{1}{3} \times \text{3,00}}{\cancelto{4}{12}} = \frac{3,00}{4} = \text{0,75} $

Palmito: 300 g para 6 porções, logo 50 g para 1 porção.

$ \begin{align} 300 \text{ g} & \propto \text{15,00} \\ 50 \text{ g} & \propto x \\ \end{align}\\ x = \displaystyle \frac{\cancelto{1}{50} \times \text{15,00}}{\cancelto{6}{300}} = \frac{15,00}{6} = \text{2,50} $

Vinagre balsâmico: 300 ml para 20 porções, logo 15 ml para 1 porção.

$ \begin{align} 500 \text{ ml} & \propto \text{40,00} \\ 15 \text{ ml} & \propto x \\ \end{align}\\ x = \displaystyle \frac{\cancelto{3}{15} \times \text{40,00}}{\cancelto{100}{500}} = \frac{120,00}{100} = \text{1,20} $

Azeite de oliva: 40 ml para 2 porções, logo 20 ml para 1 porção.

$ \begin{align} 750 \text{ ml} & \propto \text{30,00} \\ 20 \text{ ml} & \propto x \\ \end{align}\\ x = \displaystyle \frac{20 \times \cancelto{\text{1,00}}{\text{30,00}}}{\cancelto{25}{750}} = \frac{20,00}{25} = \text{0,80} $

Resumo:

$ \begin{array}{|l|r|} \hline \text{Rúcula} & 0,52 \\ \text{Alface} & 0,40 \\ \text{Queijo minas} & 3,00 \\ \text{Tomate cereja} & 1,15 \\ \text{Ovos de codorna} & 0,75 \\ \text{Palmito} & 2,50 \\ \text{Vinagre balsâmico} & 1,20 \\ \text{Azeite de oliva} & 0,80 \\ \hline \text{Total} & 10,32\\ \hline \end{array}
$

Resposta: Alternativa (B)

Questão 10

Um trem com 400 assentos tem por regra que todos os passageiros viajem sentados, que cada assento seja ocupado por somente um passageiro e que não haja o desembarque fora das estações.

– Certo dia, o trem chegou sem nenhum passageiro à estação A, na qual embarcaram exatamente 240 passageiros.

– Na estação B, primeira parada após a estação A, desembarcaram 25% dos passageiros que havia no trem e, em seguida, embarcou $ \displaystyle \frac{1}{4} $ da quantidade de passageiros que haviam permanecido no trem.

– Seguindo viagem, na estação C, próxima parada após a estação B, na qual desembarcaram $ \displaystyle \frac{2}{5} $ dos passageiros que estavam no trem e, em seguida, embarcou $ \displaystyle \frac{1}{2} $ da quantidade de passageiros que haviam desembarcado nessa parada.

– Finalmente, na estação D, próxima parada após a estação C, desembarcaram $ \displaystyle \frac{3}{10} $ dos passageiros que ainda restavam no trem e, em seguida, embarcou o triplo de passageiros que havia desembarcado nessa parada.

Após ter saído da estação D, onde fez sua terceira parada, pode-se afirmar que o número de assentos vagos no trem era:

(A) 102

(B) 288

(D) 188

(E) 112

Resolução

Vamos avaliar a sequência de estações, contabilizando cuidadosamente o quanto de passageiros que saem e que entram.

Estação A: Não desembarcou ninguém porque é a primeira estação, e embarcaram 240 passageiros.

Estação B: Desembarcaram 25% de 240, que é 1/4 deles, ou seja, desembarcaram 60 passageiros, logo restaram 240 - 60 = 180 passageiros. Embarcaram 1/4 dos que restaram, ou seja, 1/4 de 180 = 45, logo partiram 180 + 45 = 225 passageiros da estação B.

Estação C: Desembarcaram 2/5 de 225, ou seja, 90 passageiros, então permaneceram 225 - 90 = 135 passageiros. Embarcaram 1/2 de 90 (1/2 dos que desembarcaram), ou seja, 45 passageiros, logo partiram 135 + 45 = 180 passageiros da estação C.

Estação D: Desembarcaram 3/10 de 180, ou seja, 54 passageiros, restando 180 - 54 = 126 passageiros. Embarcaram 3 vezes 54 (triplo dos que desembarcaram), ou seja, 162. Assim, partiram da estação D 126 + 162 = 288 passageiros.

A questão pede a quantidade de assentos vazios. Como são 400 assentos no total, restam 400 - 288 = 112 assentos vagos.

Resposta: Alternativa (E)

Questão 11

Em uma savana, um predador avistou uma presa a 47,5 metros de distância. No mesmo instante em que o predador iniciou a corrida para caçá-la, ela iniciou a corrida para fugir dele. Ambos correndo sempre no mesmo sentido, mesma direção e em linha reta, a cada segundo o predador e a presa percorreram os espaços conforme a tabela a seguir:

\[ \begin{array}{|c|c|c|c|} \hline & \text{1º segundo} & \text{2º segundo} & \text{3º segundo} & ... \\ \hline \text{predador} & \text{15 dm} & \text{18,5 dm} & \text{22 dm} & ... \\ \hline \text{presa} & \text{150 cm} & \text{160 cm} & \text{170 cm} & ... \\ \hline \end{array} \]

Considere que os espaços percorridos a cada segundo seguiram sempre o padrão apresentado na tabela e desconsidere o tamanho do predador e da presa.

O predador alcançou a presa após ele ter percorrido quantos metros?

(A) 47,5 metros.

(B) 49,0 metros.

(D) 96,5 metros.

(E) 97,0 metros.

Resolução

Olhando para o padrão do predador: 18,5 - 15 = 3,5 dm, e 22 - 18,5 = 3,5 dm. OK, é um padrão mesmo, de 3,5 dm a cada segundo, ou velocidade de 35 cm/s.

Agora para a presa: 160 - 150 = 10 cm, e 170 - 160 = 10 cm, logo uma velocidade de 10 cm/s.

Faz sentido que como a velocidade do predador é maior que o da presa, em algum momento o predador alcança a presa. Podemos pensar na velocidade relativa entre eles, que é de 35 - 10 = 25 cm/s. O tempo que o predador alcança a presa é o mesmo tempo que um predador com velocidade de 25 cm/s alcança uma presa que está parada quando ela estava naquela distância incial.

Assim, chegamos no tempo total para o predador alcaçar a presa (usando esta velocidade relativa e a distância inicial). 47,50 m = 4750 cm

Velocidade = Distancia / Tempo

Tempo = Distancia / Velocidade = 4750 cm / (25 cm/s) = 190 s

Agora vamos calcular a distância real que o predador percorreu (usando a velocidade real e o tempo total):

Velocidade = Distancia / Tempo

Distancia = Velocidade x Tempo = 35 cm/s x 190 s = 6650 cm = 66,50 m

O gabarito oficial diz que a alternativa correta é a (D), mas não concordo.

Questão 12

Na malha quadriculada a seguir, está representada parte da cidade onde Rita mora com sua filha. As linhas representam as ruas da cidade e os quadrados da malha representam os quarteirões. Ao caminhar pelas ruas da cidade, uma pessoa percorre 200m a cada lado do quarteirão, como mostrado na figura. Na malha também estão identificados alguns locais que fazem parte da rotina de Rita e de sua filha, como pode ser observado a seguir.

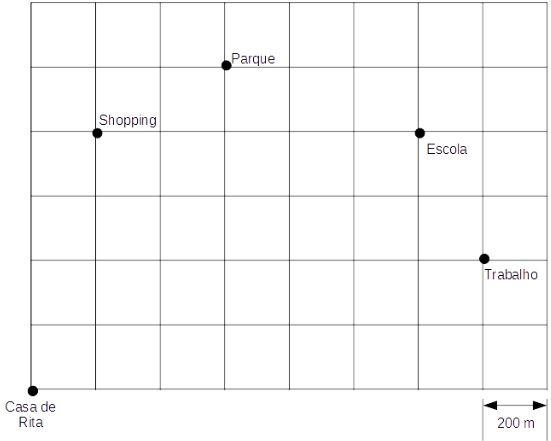
Curiosa para saber a distância que percorre semanalmente, Rita elaborou uma lista com sua rotina semanal. De segunda a sexta-feira, Rita sai de casa para o trabalho e do trabalho passa para pegar a filha na escola, voltando diretamente para casa. No sábado, Rita vai de casa até o parque com a sua filha e retorna diretamente para casa. No domingo, Rita vai até o shopping e retorna diretamente para casa.

A fim de cumprir sua rotina, Rita percorre sempre a menor distância, andando pela calçada e sem atravessar o quarteirão pelo meio (diagonal). Assim, em uma semana completa (de domingo a sábado), sem alterações de rotina, Rita percorre um total de:

(A) 27.200 km.

(B) 27,2 m.

(D) 9.600 km.

(E) 9,6 km.

Resolução

Para ir de um lugar para outro, como por exemplo, de casa para o trabalho, Rita pode seguir vários trajetos possíveis, mas só importa para nós o número mínimo de quadras que ela anda. Por exemplo, nesses 3 trajetos:

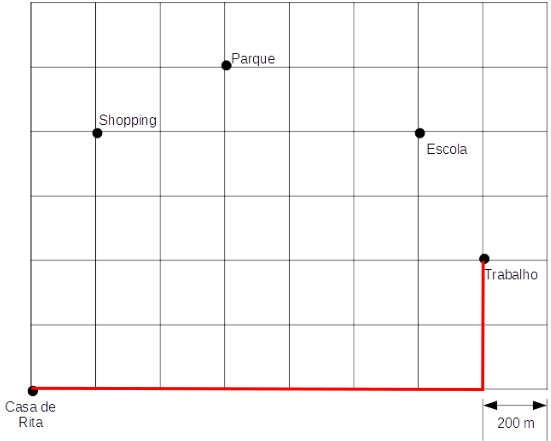
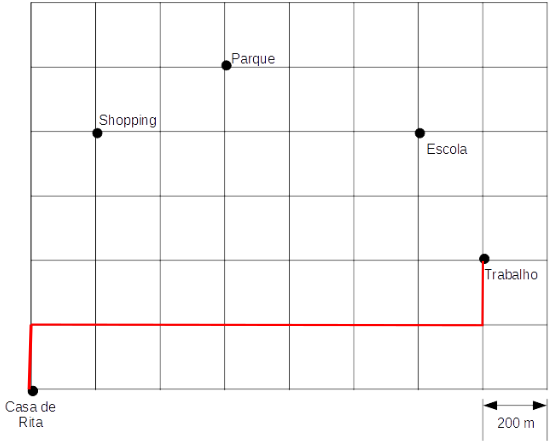
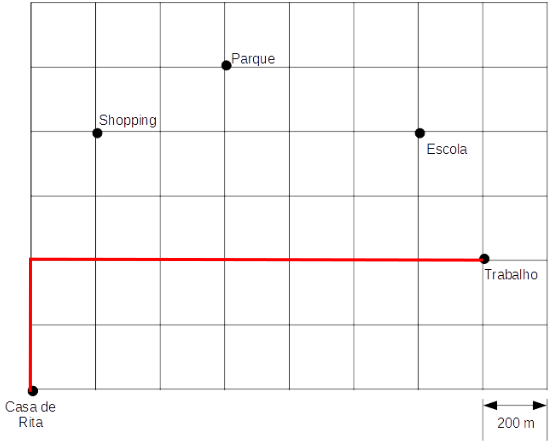
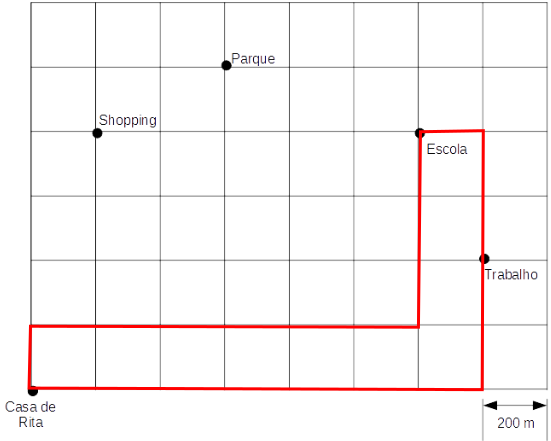
A distância percorrida é a mesma, pois Rita andou 2 quadras para "cima" e 7 quadras apara a "direita", totalizando 9 quadras. Este tipo de distância é chamada de distância Manchester.

Existem outros trajetos de mínima distância possíveis, vamos escolher apenas 1 deles para fazer a resolução, bastando que ao ir de um local para outro, não se "volte" uma quadra para uma direção oposta.

Assim, vamos traçar um trajeto para os dias úteis, um para o sábado e um para o domingo.

Dias úteis (22 quadras, ou 4.400 m cada dia):

Sábado (16 quadras, ou 3.200 m):

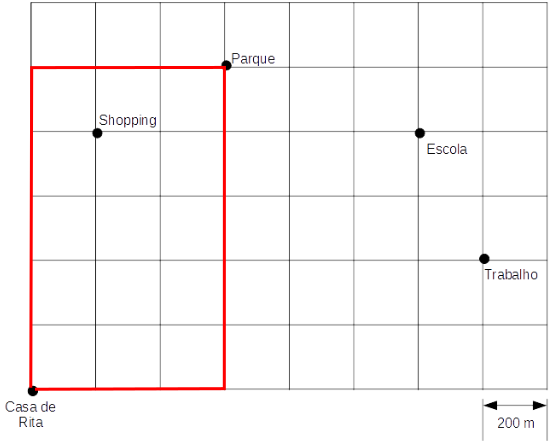
Domingo (10 quadras, ou 2.000 m):

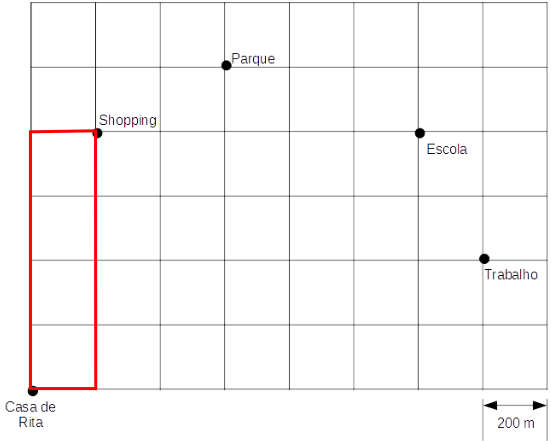
Assim, são 5 x 4.400 + 3.200 + 2.000 = 22.000 + 5.200 = 27.200 m percorridos durante toda a semana. Não existe a alternativa com 27.200 m, mas existe a 27.2 km, que é a mesma coisa.

Resposta: Alternativa (C)

Questão 13

Guilherme possui 8 miniaturas de carrinhos de modelos distintos, sendo 2 vermelhos, 2 amarelos e 4 azuis. De quantas maneiras diferentes Guilherme pode organizar seus carrinhos sobre uma prateleira horizontal, de maneira que todos fiquem de frente para ele, um ao lado do outro, à mesma distância entre cada um deles e de modo que os carrinhos de mesma cor permaneçam juntos?

(A) 72

(B) 96

(D) 216

(E) 576

Resolução

Podemos usar o Princípio Fundamental da Contagem (PFC), para calcular todas estas possíveis maneiras diferentes. São 4 etapas independentes:

Escolha da ordem das 3 cores
Escolha da ordem dos carrinhos vermelhos
Escolha da ordem dos carrinhos amarelos
Escolha da ordem dos carrinhos azuis

Primeiro pensamos em como ordenar as 3 cores:

Vermelho - Amarelo - Azul
Vermelho - Azul - Amarelo
Amarelo - Azul - Vermelho
Amarelo - Vermelho - Azul
Azul - Amarelo - Vermelho
Azul - Vermelho - Amarelo

Só existem estas 6 formas, que também poderíamos pensar que são as 6 permutações possívesis de 3 elementos. $ P_3 = 3! = 3 \cdot 2 \cdot 1 = 6 $.

Já entre os carrinhos de mesma cor, eles são diferentes entre si, pois foi dito que os 8 carrinhos possuem modelos diferentes. Assim, na escolha de quantas formas podemos ordená-los, basta ver quantas permutações de X elementos ($P_X$) podemos calcular. Aqui X é o número de elementos da cor que queremos ordenar.

Vermelho: $ P_2 = 2! = 2 \cdot 1 = 2 $

Amarelo: $ P_2 = 2! = 2 \cdot 1 = 2 $

Azul: $ P_4 = 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 $

Portanto, conseguimos calcular as quantidade de formas possíveis para cada etapa. Aplicando o PFC, chegamos que são $ 6 \cdot 2 \cdot 2 \cdot 24 = 576$ formas de se ordenar os 8 carrinhos seguindo as condições dadas.

Resposta: Alternativa (E)

Questão 14

Um garoto aproveitou o tempo livre no apartamento onde mora e resolveu montar casinhas em forma de pentágono, utilizando palitos de fósforo, seguindo o padrão ilustrado na figura abaixo. O primeiro pentágono tem lado medindo o comprimento de um palito de fósforo, o segundo tem lado medindo dois palitos de fósforo, o terceiro tem lado medindo três palitos de fósforo e assim por diante, sempre aumentando a medida do lado em um palito de fósforo de uma figura para a outra.

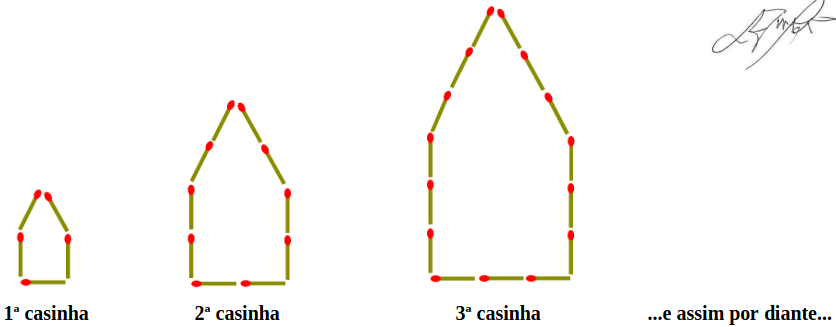
O garoto construiu casinhas até que os fósforos que sobraram não eram suficientes para construir a próxima casinha.

Sabe-se que:

I - uma caixa de fósforos cheia tem 40 palitos cada;

II - a primeira caixa de fósforos que o garoto utilizou tinha somente $ \displaystyle \frac{5}{8} $ do total de palitos;

III - sem desmanchar nenhuma casinha já montada, o garoto conseguiu construir 15 delas.

Considerando a situação descrita e as informações apresentadas, pode-se afirmar que o garoto tinha:

(A) 14 caixas de fósforo completamente cheias e faltaram 25 palitos de fósforo para ele montar a 16ª casinha.

(B) 14 caixas de fósforo completamente cheias e faltaram 55 palitos de fósforo para ele montar a 16ª casinha.

(D) 15 caixas de fósforo completamente cheias e faltaram 55 palitos de fósforo para ele montar a 16ª casinha.

(E) 15 caixas de fósforo completamente cheias e faltaram 80 palitos de fósforo para ele montar a 16ª casinha.

Resolução

Observe que o pentágono que forma a primeira casinha utiliza 5 palitos, na segunda casinha são 10 palitos, na terceira são 15 palitos, e assim por diante. Com isso, sabemos que a casinha na posição n utiliza-se de 5n palitos, ou seja, a 15ª casinha utiliza 75 palitos e a 16ª casinha utiliza 80 palitos.

A sequência de palitos crescentes 5, 10, 15, ..., 75 é uma P.A. de termo inicial 5 e razão 5 e 15 termos. Assim, vamos calcular a quantidade de palitos totais para formar 16 casinhas:

$\require{cancel}$

$ S_n = \displaystyle \frac{(a_1 + a_n) \cdot n}{2} \ $

$ S_{15} = \displaystyle \frac{(5 + 75) \cdot 15}{2} = \frac{\cancelto{40}{80} \cdot 15}{\cancelto{1}{2}} = 40 \cdot 15 = 600 $

Sendo 600 palitos para 15 casinhas e 40 palitos por caixa, necessitamos de $600 \div 40 = 15$ caixas. Mas a primeira caixa possuía somente $\displaystyle \frac{5}{8}$ dos palitos, ou seja, $\displaystyle \frac{5}{8} \times 40 = 25$ palitos, logo precisamos desta primeira caixa incompleta mais 15 caixas cheias para conseguir montar as 15 casinhas, sobrando justamente 25 palitos na última caixa. Como a 16ª casinha precisaria de 80 palitos, faltaram 55 palitos para esta casa.

Assim, a alternativa correta é a D

Resposta: Alternativa (D)

Questão 15

Estela teve a ideia de construir um quadrado mágico utilizando alguns cartões que traziam a representação de números. Observe a seguir os onze cartões que ela possuía, considerando que eles são quadrados e não estão em escala:

Estela escolheu nove dos onze cartões que possuía, organizando-os, sem nenhuma repetição, em um quadrado mágico com três linhas e três colunas, como representado abaixo.

Nesse quadrado mágico, a soma dos valores dos três números dispostos em cada linha, em cada coluna e em cada diagonal é igual a $ \displaystyle 9\frac{3}{4} $. Na posição central, segunda linha e segunda coluna, Estela colocou o valor correspondente a $ \displaystyle \frac{1}{3} $ da soma. Dispondo corretamente os nove números escolhidos, a fim de que a soma $ \displaystyle 9\frac{3}{4} $ seja satisfeita em todos os casos, a alternativa que apresenta os dois números não escolhidos por Estela é:

(A) $ \displaystyle 3\frac{3}{4} $ e $ \displaystyle 1\frac{3}{4} $

(B) $ \displaystyle 5\frac{1}{4} $ e $ 2 $

(D) $ \displaystyle 2\frac{3}{4} $ e $ 4 $

(E) $ \displaystyle 1\frac{1}{4} $ e $ \displaystyle 4\frac{1}{2} $

Resolução

Antes, vamos esclarecer que esta notação de $ \displaystyle 9\frac{3}{4} $ (nove e três quartos) não é a mesma coisa que $ \displaystyle 9 \cdot \frac{3}{4} = \frac{27}{4} $, e sim, igual a $ \displaystyle 9 + \frac{3}{4} $.

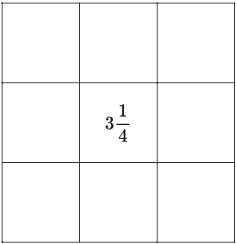
Vamos colocar primeiro o valor central deste quadrado mágico. Sendo $ \displaystyle \frac{1}{3} $ de $ \displaystyle 9\frac{3}{4} $, isso é igual a $ \displaystyle 3\frac{1}{4} $.

Agora, sabemos que a soma dos outros 2 valores na mesma linha/coluna/diagonal precisa ser igual a $ \displaystyle \frac{2}{3} $ de $ \displaystyle 9\frac{3}{4} $, ou seja, $ \displaystyle 6\frac{1}{2} $. Assim, vamos analisar se para cada um dos cartões restantes existe um outro cartão que faz com que a soma destes 2 cartões resulte em $ \displaystyle 6\frac{1}{2} $.

$2$: $ \displaystyle 6\frac{1}{2} - 2 = 4\frac{1}{2}$. Bom, eliminamos o $\displaystyle 4\frac{1}{2}$ aqui.

$\displaystyle 1\frac{1}{4} $: $ \displaystyle 6\frac{1}{2} - 1\frac{1}{4} = 5\frac{1}{4}$. E aqui eliminamos o $\displaystyle 5\frac{1}{4}$.

$\displaystyle 3\frac{3}{4} $: $ \displaystyle 6\frac{1}{2} - 3\frac{3}{4} = 2\frac{3}{4}$. E aqui eliminamos o $\displaystyle 2\frac{3}{4}$.

$\displaystyle 3\frac{1}{2} $: $ \displaystyle 6\frac{1}{2} - 3\frac{1}{2} = 3$. como não tem cartão com valor 3, então sabemos que o $\displaystyle 3\frac{1}{2} $ é um dos cartões que não pode ser utilizado.

$\displaystyle 2\frac{1}{2} $: $ \displaystyle 6\frac{1}{2} - 2\frac{1}{2} = 4$. E aqui eliminamos o 4.

Portanto, os 2 cartões que não podem ser utilizados são o $\displaystyle 3\frac{1}{2} $ e o $\displaystyle 1\frac{3}{4} $

Resposta: Alternativa (C)

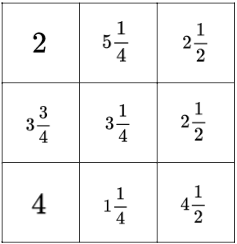
Extra: Aqui está um quadrado mágico possível com os 9 cartões escolhidos:

Questão 16

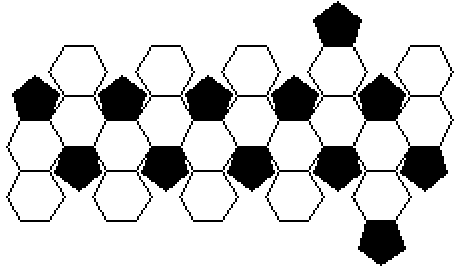
Uma bola de futebol pode ser representada por um poliedro convexo cujo nome é icosaedro truncado. Esse poliedro é constituído de 20 faces hexagonais e 12 faces pentagonais cujos lados são todos congruentes entre si. Uma possível planificação desse sólido é ilustrada a seguir.

Sabendo-se que nesse poliedro convexo o número de vértices é $ \displaystyle \frac{2}{3} $ do número de arestas, é incorreto afirmar que:

(A) o icosaedro truncado possui 60 vértices e 90 arestas.

(B) se cada aresta medisse 8 cm, a soma das medidas de todas as arestas alinhadas seria 7,2 m.

(D) a diferença entre o número de arestas e de faces do icosaedro truncado é 60.

(E) o icosaedro truncado possui mais arestas do que vértices.

Resolução

Temos que analisar cada afirmação e verificar a veracidade. Antes de tudo, vamos entender de onde é que veio essa idéia de "icosaedro truncado". Um icosaedro normal é um poliedro de 20 faces triangulares.

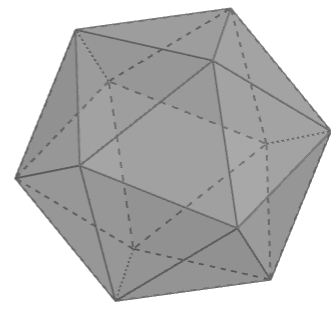
Cada vértice é conectado a 5 arestas, logo podemos pensar em remover pirâmides de base pentagonal a partir de cada um desses vértices, resultando em faces pentagonais e hexagonais.

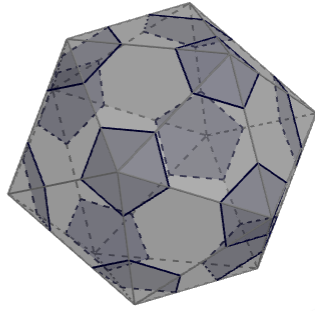
E assim chegamos no icosaedro truncado, e é sempre possível recortar as pirâmides de forma que todas as arestas fiquem do mesmo tamanho.

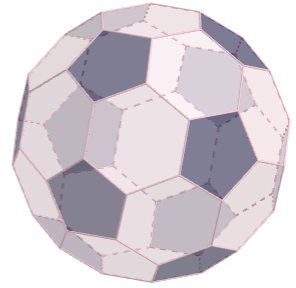
Bom, vamos às afirmações. Como $V = \displaystyle \frac{2A}{3}$, então a afirmação (E) é verdadeira de cara, pois ela diz que $A > V$. Também sabemos que 20 faces hexagonais mais 12 faces pentagonais resultam em 32 faces totais, logo (C) também é verdadeira. Agora precisamos saber a quantidade de arestas e vértices.

Como este icosaedro truncado é um poliedro convexo, vale a relação de Euler:

$V + F = A + 2$

V: número de vértices

F: número de faces

A: número de arestas

Novamente, aplicando as relações conhecidas:

$\displaystyle \frac{2A}{3} + 32 = A + 2$

$32 - 2 = A - \displaystyle \frac{2A}{3}$

$30 = \displaystyle \frac{A}{3}$

$A = 90$

$V = \displaystyle \frac{2A}{3} = \frac{2 \cdot 90}{3} = 60$

Com isso, a afirmação (A) é verdadeira.

Sabendo que são 90 arestas, caso elas medissem 8 cm cada, a soma dos comprimentos das arestas seria de $90 \cdot 8 = 720$ cm, ou 7,2 m. Portanto, a afirmação (B) é verdadeira.

Só restou então verificar a (D), que afirma que $A - F = 60$, o que é falso, já que $A = 90$ e $F = 32$, logo $A - F = 58$.

Resposta: Alternativa (D)

Questão 17

Em uma turma de alunos que se preparavam para o concurso de admissão ao Colégio Militar, o professor apresentou o problema abaixo:

“Pensei em um número de três algarismos diferentes que estão escritos da esquerda para a direita, em ordem decrescente. Quando troco de posição o algarismo das centenas com o das unidades simples e subtraio do número pensado, a diferença é 594. Por outro lado, quando troco de posição o algarismo das dezenas com o das unidades simples do número pensado, o número diminui em 9 unidades. Sabe-se também que a soma de todos os algarismos desse número é 13.”

Após determinar o número pensado pelo professor, é correto afirmar que a soma desse número pensado com o maior número de três algarismos distintos é:

(A) 1.918

(B) 1.828

(D) 1.738

(E) 1.729

Questão 18

Um relógio defeituoso adianta 120 segundos a cada 10 minutos. Quando, no horário de Brasília, eram três horas e trinta e três minutos, Ricardo acertou o relógio para esse horário. A partir daí, depois de transcorrido um período de seis horas, Ricardo olhou novamente para o relógio defeituoso e viu que ele indicava:

(A)

(B)

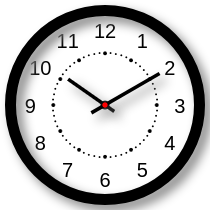
(C)

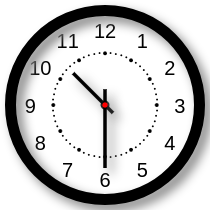
(D)

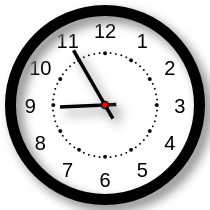
(E)

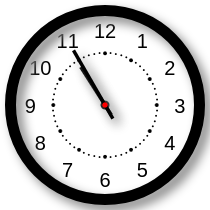
Questão 19

João Lucas gostava muito de solucionar exercícios relacionados a sólidos geométricos e resolveu aceitar um desafio de seu professor: encontrar a resposta para uma expressão numérica.

Nas figuras, a seguir, estão apresentados três sólidos geométricos.

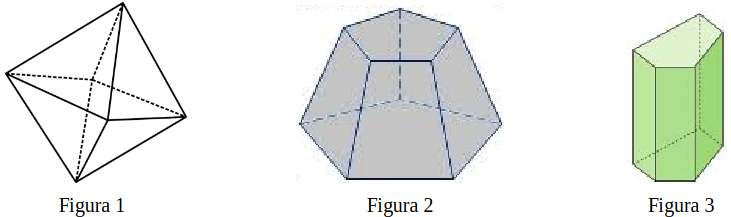
Considere:

– A o número de arestas da figura 1;

– B o número de vértices da figura 2; e

– C o número de faces da figura 3.

Observe agora a representação de A, B e C na expressão numérica a seguir.

\[ \frac{C}{9} \div \left( \frac{\text{1,5} + \displaystyle \frac{2}{3} - \frac{9}{6} - \frac{2}{A}}{\text{1,6} \times \displaystyle \frac{3}{8} \div 2 + 1 + \text{0,5}} + \frac{1}{3} \times \frac{5}{B}\right) \]

Após resolver corretamente a expressão numérica, João Lucas encontrará como resposta o decimal:

(A) 1,75

(B) 17,5

(D) 175

(E) 0,74

Questão 20

Em uma experiência, um cientista maluco resolveu fazer os seguintes procedimentos com recipientes:

1º) encheu um primeiro recipiente em forma de bloco retangular (paralelepípedo) de 2 dm de largura, 40 cm de comprimento e 1,5 m de altura, com uma certa quantidade de água, de tal forma que o recipiente não ficou totalmente cheio;

2º) metade da quantidade de água que havia no primeiro recipiente foi despejada num segundo recipiente;

3º) em um terceiro recipiente foi despejada metade da quantidade de água que havia no segundo recipiente; e

4º) manteve o procedimento de despejar no recipiente seguinte sempre a metade da quantidade de água que havia no recipiente imediatamente anterior.

Ele manteve o experimento e percebeu que, no 10º recipiente, despejou 0,125 litros de água. Considerando que em todos os procedimentos não houve perda de água, é correto afirmar que quando o cientista colocou a água para iniciar o experimento, a altura que faltou para a água encher completamente o primeiro recipiente, foi de:

(A) 70 m.

(B) 8 dm.

(D) 70 dm.

(E) 8 cm.

Provas Colégio Militar de Curitiba (CMC) - 6º ano