Questão 6
Na malha quadriculada de 15x15 quadradinhos, ilustrada abaixo, está desenhada uma figura construída a partir das sete peças de um Tangram e identificadas cada uma com uma letra.
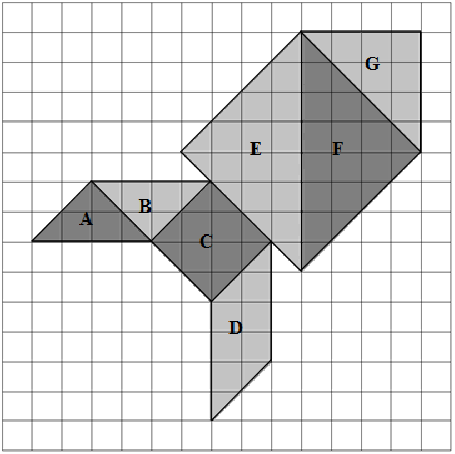
Considere que todos os quadradinhos da malha quadriculada possuem a mesma área. Observe as áreas identificadas na figura e considere as afirmações a seguir:
I - A área de F é igual à soma das áreas de A, de B e de G.
II - A área de C é 50% da área de E.
III - A área de D é 50% da soma das áreas de E e de A.
IV - A soma das áreas de E e de F é igual à soma das áreas de A, de B, de C e de D.
V - A soma das áreas de D e de A é igual à área de G.
VI - A área de G é igual à soma das áreas de A e de B.
São verdadeiras somente as afirmações:
(A) I, II, V e VI.
(B) I, II e VI.
(C) I, III, V.
(D) II, III e IV.
(E) II, V e VI.
Resolução
Resolução
Para resolver, é preciso conhecer as formas de calcular áreas de quadriláteros e triângulos.
Quadriláteros: \( \text{Área} = \text{base} \times \text{altura} \)
Triângulos: \( \text{Área} = \displaystyle \frac{\text{base} \times \text{altura}}{2}\)
Agora, vamos às figuras. Os triângulos A e B são congruentes, de base 4 e altura 2. Assim, a área de ambos é igual a \( \displaystyle \frac{4 \times 2}{2} = 4\).
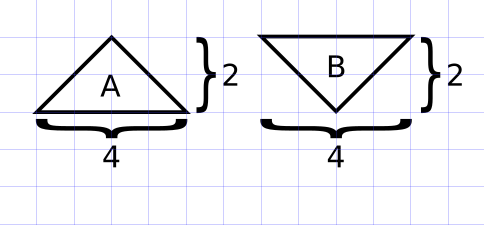
O quadrado C pode ser dividido em 2 triângulos de base 4 e altura 2, logo a área é igual a \( 2 \times \displaystyle \frac{4 \times 2}{2} = 2 \times 4 = 8\).
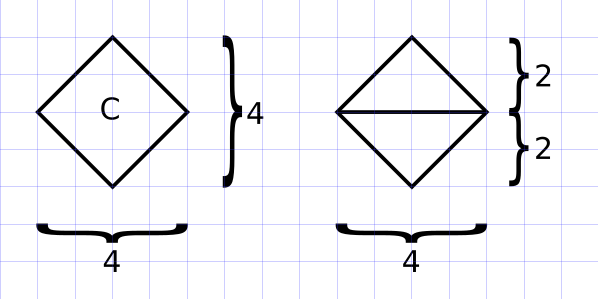
O paralelogramo D possui base 4 e altura 2, logo área igual a \(4 \times 2 = 8\).
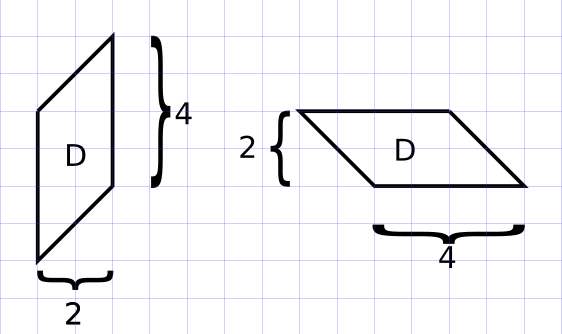
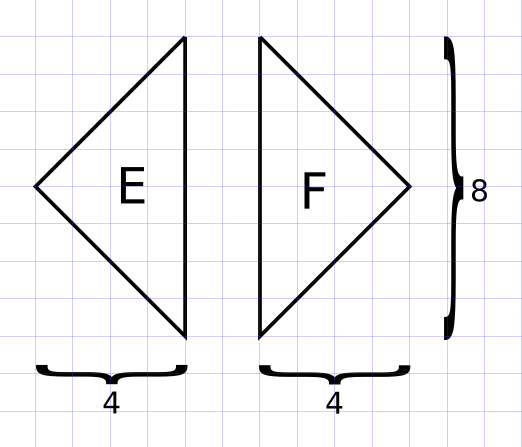
Os triângulos E e F são congruentes, de base 8 e altura 4, logo área igual a \( \displaystyle\frac{8 \times 4}{2} = 16 \).
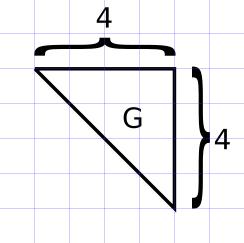
O triângulo G tem base 4 e altura 4, logo área igual a \( \displaystyle \frac{4 \times 4}{2} = 8 \).
Também podemos tabelar esses valores para avaliar mais facilmente as afirmações:
\( \begin{array}{|c|c|c|c|c|c|c|} \hline A & B & C & D & E & F & G \\ \hline 4 & 4 & 8 & 8 & 16 & 16 & 8 \\ \hline \end{array} \)
"I - A área de F é igual à soma das áreas de A, de B e de G." - Verdadeira (16 = 4 + 4 + 8)
"II - A área de C é 50% da área de E." - Verdadeira (8 = 50% de 16)
"III - A área de D é 50% da soma das áreas de E e de A." - Falsa (A + E = 4 + 16 = 20, e 50% de 20 é 10, e não 8)
"IV - A soma das áreas de E e de F é igual à soma das áreas de A, de B, de C e de D." - Falsa (E + F = 16 + 16 = 32. A + B + C = 4 + 4 + 8 = 16).
"V - A soma das áreas de D e de A é igual à área de G." - Falsa (D + A = 8 + 4 = 12, e G = 8)
"VI - A área de G é igual à soma das áreas de A e de B." - Verdadeira (8 = 4 + 4)
Resposta: Alternativa (B)