Questão 15

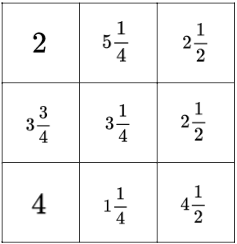
Estela teve a ideia de construir um quadrado mágico utilizando alguns cartões que traziam a representação de números. Observe a seguir os onze cartões que ela possuía, considerando que eles são quadrados e não estão em escala:

Estela escolheu nove dos onze cartões que possuía, organizando-os, sem nenhuma repetição, em um quadrado mágico com três linhas e três colunas, como representado abaixo.

Nesse quadrado mágico, a soma dos valores dos três números dispostos em cada linha, em cada coluna e em cada diagonal é igual a \( \displaystyle 9\frac{3}{4} \). Na posição central, segunda linha e segunda coluna, Estela colocou o valor correspondente a \( \displaystyle \frac{1}{3} \) da soma. Dispondo corretamente os nove números escolhidos, a fim de que a soma \( \displaystyle 9\frac{3}{4} \) seja satisfeita em todos os casos, a alternativa que apresenta os dois números não escolhidos por Estela é:

(A) \( \displaystyle 3\frac{3}{4} \) e \( \displaystyle 1\frac{3}{4} \)

(B) \( \displaystyle 5\frac{1}{4} \) e \( 2 \)

(C) \( \displaystyle 3\frac{1}{2} \) e \( \displaystyle 1\frac{3}{4} \)

(D) \( \displaystyle 2\frac{3}{4} \) e \( 4 \)

(E) \( \displaystyle 1\frac{1}{4} \) e \( \displaystyle 4\frac{1}{2} \)

Resolução

Antes, vamos esclarecer que esta notação de \( \displaystyle 9\frac{3}{4} \) (nove e três quartos) não é a mesma coisa que \( \displaystyle 9 \cdot \frac{3}{4} = \frac{27}{4} \), e sim, igual a \( \displaystyle 9 + \frac{3}{4} \).

Vamos colocar primeiro o valor central deste quadrado mágico. Sendo \( \displaystyle \frac{1}{3} \) de \( \displaystyle 9\frac{3}{4} \), isso é igual a \( \displaystyle 3\frac{1}{4} \).

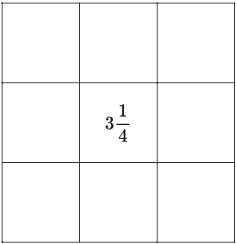
Agora, sabemos que a soma dos outros 2 valores na mesma linha/coluna/diagonal precisa ser igual a \( \displaystyle \frac{2}{3} \) de \( \displaystyle 9\frac{3}{4} \), ou seja, \( \displaystyle 6\frac{1}{2} \). Assim, vamos analisar se para cada um dos cartões restantes existe um outro cartão que faz com que a soma destes 2 cartões resulte em \( \displaystyle 6\frac{1}{2} \).

\(2\): \( \displaystyle 6\frac{1}{2} - 2 = 4\frac{1}{2}\). Bom, eliminamos o \(\displaystyle 4\frac{1}{2}\) aqui.

\(\displaystyle 1\frac{1}{4} \): \( \displaystyle 6\frac{1}{2} - 1\frac{1}{4} = 5\frac{1}{4}\). E aqui eliminamos o \(\displaystyle 5\frac{1}{4}\).

\(\displaystyle 3\frac{3}{4} \): \( \displaystyle 6\frac{1}{2} - 3\frac{3}{4} = 2\frac{3}{4}\). E aqui eliminamos o \(\displaystyle 2\frac{3}{4}\).

\(\displaystyle 3\frac{1}{2} \): \( \displaystyle 6\frac{1}{2} - 3\frac{1}{2} = 3\). como não tem cartão com valor 3, então sabemos que o \(\displaystyle 3\frac{1}{2} \) é um dos cartões que não pode ser utilizado.

\(\displaystyle 2\frac{1}{2} \): \( \displaystyle 6\frac{1}{2} - 2\frac{1}{2} = 4\). E aqui eliminamos o 4.

Portanto, os 2 cartões que não podem ser utilizados são o \(\displaystyle 3\frac{1}{2} \) e o \(\displaystyle 1\frac{3}{4} \)

Resposta: Alternativa (C)

Extra: Aqui está um quadrado mágico possível com os 9 cartões escolhidos: