Questão 16

Uma bola de futebol pode ser representada por um poliedro convexo cujo nome é icosaedro truncado. Esse poliedro é constituído de 20 faces hexagonais e 12 faces pentagonais cujos lados são todos congruentes entre si. Uma possível planificação desse sólido é ilustrada a seguir.

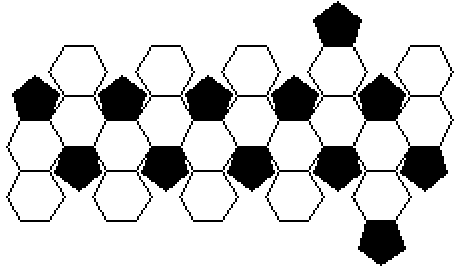
Sabendo-se que nesse poliedro convexo o número de vértices é \( \displaystyle \frac{2}{3} \) do número de arestas, é incorreto afirmar que:

(A) o icosaedro truncado possui 60 vértices e 90 arestas.

(B) se cada aresta medisse 8 cm, a soma das medidas de todas as arestas alinhadas seria 7,2 m.

(C) o icosaedro truncado possui 32 faces no total.

(D) a diferença entre o número de arestas e de faces do icosaedro truncado é 60.

(E) o icosaedro truncado possui mais arestas do que vértices.

Resolução

Temos que analisar cada afirmação e verificar a veracidade. Antes de tudo, vamos entender de onde é que veio essa idéia de "icosaedro truncado". Um icosaedro normal é um poliedro de 20 faces triangulares.

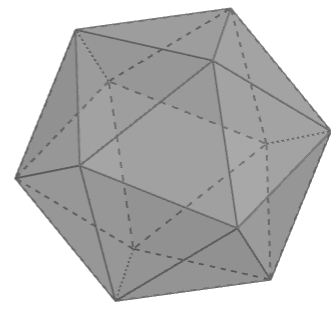
Cada vértice é conectado a 5 arestas, logo podemos pensar em remover pirâmides de base pentagonal a partir de cada um desses vértices, resultando em faces pentagonais e hexagonais.

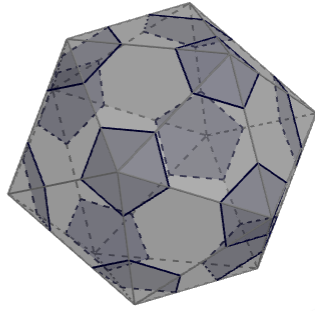
E assim chegamos no icosaedro truncado, e é sempre possível recortar as pirâmides de forma que todas as arestas fiquem do mesmo tamanho.

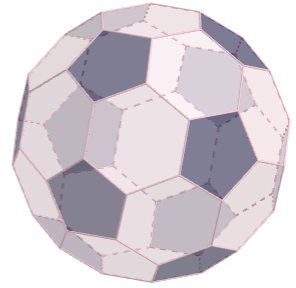
Bom, vamos às afirmações. Como \(V = \displaystyle \frac{2A}{3}\), então a afirmação (E) é verdadeira de cara, pois ela diz que \(A > V\). Também sabemos que 20 faces hexagonais mais 12 faces pentagonais resultam em 32 faces totais, logo (C) também é verdadeira. Agora precisamos saber a quantidade de arestas e vértices.

Como este icosaedro truncado é um poliedro convexo, vale a relação de Euler:

\(V + F = A + 2\)

V: número de vértices

F: número de faces

A: número de arestas

Novamente, aplicando as relações conhecidas:

\(\displaystyle \frac{2A}{3} + 32 = A + 2\)

\(32 - 2 = A - \displaystyle \frac{2A}{3}\)

\(30 = \displaystyle \frac{A}{3}\)

\(A = 90\)

\(V = \displaystyle \frac{2A}{3} = \frac{2 \cdot 90}{3} = 60\)

Com isso, a afirmação (A) é verdadeira.

Sabendo que são 90 arestas, caso elas medissem 8 cm cada, a soma dos comprimentos das arestas seria de \(90 \cdot 8 = 720\) cm, ou 7,2 m. Portanto, a afirmação (B) é verdadeira.

Só restou então verificar a (D), que afirma que \(A - F = 60\), o que é falso, já que \(A = 90\) e \(F = 32\), logo \(A - F = 58\).

Resposta: Alternativa (D)